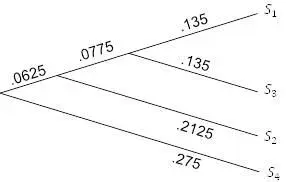
Рисунок 5.8. UPGMA; шаг 3.
Как и подозревали, дерево, которое построили для имеющихся данных, не совсем соответствует этим данным. Расстояние на дереве от 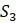 до
до 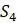 , например, равно
, например, равно 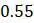 , хотя по исходным данным должно быть
, хотя по исходным данным должно быть 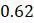 . Тем не менее, расстояния между вершинами построенного дерева, по крайней мере, достаточно близки к расстояниям, указанным в исходных табличных данных.
. Тем не менее, расстояния между вершинами построенного дерева, по крайней мере, достаточно близки к расстояниям, указанным в исходных табличных данных.
Если бы было больше таксонов, то пришлось бы сделать больше шагов для завершения процесса UPGMA, но не было бы никаких принципиально новых действий. На каждом шаге объединяем два ближайших таксона или группы вместе, всегда размещая их на равных расстояниях от общего предка. Затем сворачиваем объединенные таксоны в группу, используя усреднение для вычисления расстояния от этой группы до таксонов и групп, которые еще предстоит объединить. Один момент, с которым следует быть особенно осторожным, заключается в том, что при вычислении расстояний между двумя группами нужно усреднить все расстояния от членов одной группы до членов другой – если одна группа имеет 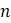 членов, а другая имеет
членов, а другая имеет 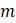 членов, придется усреднить
членов, придется усреднить 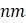 расстояний. Каждый шаг алгоритма уменьшает размер таблицы расстояний на единицу, так что после достаточного количества шагов все таксоны объединяются в единое дерево.
расстояний. Каждый шаг алгоритма уменьшает размер таблицы расстояний на единицу, так что после достаточного количества шагов все таксоны объединяются в единое дерево.
Обратите внимание, что предположение о молекулярных часах неявно присутствовала в UPGMA. В примере, когда поместили 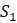 и
и 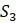 на концы ветвей одинаковой длины, предположили, что количество мутаций, которые каждый из них претерпел от своего общего предка, было одинаковым. Метод UPGMA всегда размещает все таксоны на одинаковом расстоянии от корня, так что количество мутаций от корня до любого таксона одинаково.
на концы ветвей одинаковой длины, предположили, что количество мутаций, которые каждый из них претерпел от своего общего предка, было одинаковым. Метод UPGMA всегда размещает все таксоны на одинаковом расстоянии от корня, так что количество мутаций от корня до любого таксона одинаково.
Вторым рассмотрим алгоритм Фитча-Марголиаша. Этот метод немного сложнее, чем UPGMA, но основан на том же подходе. Тем не менее, попытаемся отказаться от предположения UPGMA о молекулярных часах.
Прежде чем изложить алгоритм, сделаем несколько математических наблюдений. Во-первых, если попытаемся поместить 3 таксона на некорневое дерево, то будет только одна топология, которую необходимо учитывать. Кроме того, для 3 таксонов можем назначить желаемые длины ребер, чтобы точно соответствовать данным. Чтобы убедиться в этом, рассмотрим дерево на рисунке 5.9. Если есть некоторые данные о расстоянии 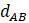 ,
, 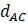 и
и 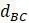 , то можно составить систему уравнений
, то можно составить систему уравнений 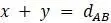 ,
, 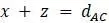 ,
, 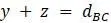 .
.
Эти уравнения могут быть решены либо путем записи системы в виде матричного уравнения и нахождения обратной матрицы, либо путем подстановки формулы для одной переменной, полученной из одного уравнения, в другие. Любой способ гарантированно приведёт к следующему решению 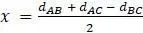 ,
, 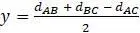 ,
, 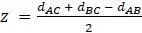 .
.
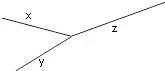
Рисунок 5.9. Некорневое 3-таксонное дерево.
Будем называть эти формулы 3-точечными формулами для подгонки таксонов к дереву. К сожалению, с более чем 3 таксонами точная подгонка данных к дереву обычно невозможна. Однако алгоритм Фитча-Марголиаша (кратко называемый в таблицах как FM) использует случай 3 таксонов для обработки большего количества таксонов. Теперь объясним работу алгоритма на примере. Будем использовать данные о расстоянии, приведенные в таблице 5.4.
Читать дальше


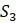 до
до 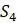 , например, равно
, например, равно 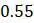 , хотя по исходным данным должно быть
, хотя по исходным данным должно быть 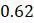 . Тем не менее, расстояния между вершинами построенного дерева, по крайней мере, достаточно близки к расстояниям, указанным в исходных табличных данных.
. Тем не менее, расстояния между вершинами построенного дерева, по крайней мере, достаточно близки к расстояниям, указанным в исходных табличных данных.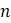 членов, а другая имеет
членов, а другая имеет 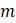 членов, придется усреднить
членов, придется усреднить 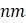 расстояний. Каждый шаг алгоритма уменьшает размер таблицы расстояний на единицу, так что после достаточного количества шагов все таксоны объединяются в единое дерево.
расстояний. Каждый шаг алгоритма уменьшает размер таблицы расстояний на единицу, так что после достаточного количества шагов все таксоны объединяются в единое дерево.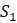 и
и 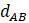 ,
, 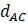 и
и 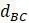 , то можно составить систему уравнений
, то можно составить систему уравнений 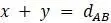 ,
, 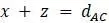 ,
, 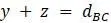 .
.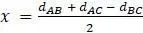 ,
, 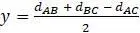 ,
, 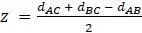 .
.











