Как правило, длины ребер в филогенетическом дереве, построенном из данных последовательности ДНК, каким-то образом представляют собой количество мутаций, которые произошли между расщеплениями линии. Чем длиннее ребро, тем больше последовательность ДНК мутировала в ходе эволюции, которую представляет это ребро.
Если, например, модель Джукса-Кантора замещения оснований адекватно описала эволюцию нескольких таксонов, то длина ребра в дереве, относящемся к ним, может быть расстоянием Джукса-Кантора между последовательностями на двух концах. Как видели в главе 4, это расстояние представляет собой среднее число замен оснований на сайт, произошедших при происхождении новой последовательности. Сюда включены мутации, скрытые другими мутациями, для оценки которых была разработана формула расстояния. Поскольку расстояние Джукса-Кантора является аддитивным и симметричным, общее расстояние между двумя таксонами вдоль дерева должно быть расстоянием Джукса-Кантора между ними.
Если предположение о молекулярных часах справедливо для эволюции связанных последовательностей, то расстояния в дереве имеют постоянное значение. Напомним, что молекулярные часы просто означают, что скорость мутаций постоянна для всех рассматриваемых линий. Если 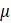 обозначает скорость мутации, измеряемую, например, в количестве произошедших за год замен оснований на сайт, а
обозначает скорость мутации, измеряемую, например, в количестве произошедших за год замен оснований на сайт, а 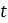 обозначает время в годах, то количество мутаций, которое произойдет в течение этого времени, составляет
обозначает время в годах, то количество мутаций, которое произойдет в течение этого времени, составляет 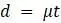 базовых замен на сайт.
базовых замен на сайт.
Таким образом, молекулярные часы означают, что количество мутаций на любом ребре пропорционально прошедшему времени, при этом константа пропорциональности представляет собой постоянную скорость мутации. Если предположить, что существуют молекулярные часы, то независимо от того, рисуем ли длины ребер, представляющие количество мутаций или только прошедшее время, то нарисуем одну и ту же фигуру с точностью до масштаба этой константы.
Если гипотеза молекулярных часов справедлива для корневого метрического дерева, то каждый лист будет расположен на одинаковом общем расстоянии от корня дерева. Это связано с тем, что расстояния от корня пропорциональны времени, прошедшему с тех пор, как таксоны начали расходиться с общим предком. У каждого таксона было одинаковое количество времени, чтобы эволюционировать от корневого предка, поэтому каждый таксон накопит одинаковое количество мутаций.
Без молекулярных часов связь между количеством мутаций вдоль ребра и количеством времени может быть сложной для моделирования. Предположим, что вдоль одного ребра филогенетического дерева частота мутаций была довольно мала, а вдоль другого – частота мутаций была большой. Затем несмотря на то, что оба края могут соответствовать одинаковому количеству времени, вдоль одного из них произойдет значительно больше мутаций. Без получения какой-либо дополнительной информации о скорости мутации – возможно, путем сравнения с летописью окаменелостей – обычно нет способов определения прошедшего времени, связанного с ребрами деревьев.
Метрические деревья иногда рисуются в «квадратном» стиле, чтобы было легче сравнивать расстояния по различным эволюционным путям. Например, два дерева на рисунке 5.4 представляют одну и ту же информацию. В дереве слева ребра имеют указанную длину, а в дереве справа горизонтальные ребра имеют те же длины. Таким образом, вертикальные ребра на правом дереве считываются как не вносящие никакого вклада в количество мутаций; они служат исключительно для разделения различных линий для повышения читабельности.
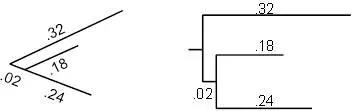
Рисунок 5.4. Разные изображения одного и того же метрического дерева.
Задачи для самостоятельного решения:
5.1.1. Рассмотрим деревья на рисунке 5.5.
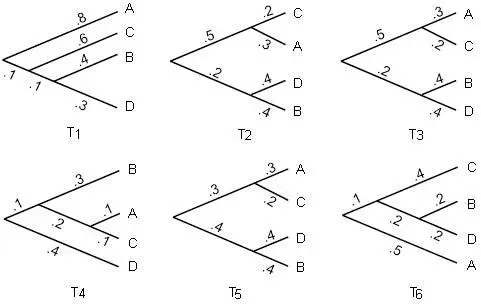
Рисунок 5.5. Деревья для задачи 5.1.1.
а. Какие из них совпадают с корневыми метрическими деревьями?
б. Какие из них совпадают с некорневыми метрическими деревьями?
в. Какие из них такие же, как корневые топологические деревья?
г. Какие из них такие же, как некорневые топологические деревья?
Читать дальше

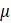 обозначает скорость мутации, измеряемую, например, в количестве произошедших за год замен оснований на сайт, а
обозначает скорость мутации, измеряемую, например, в количестве произошедших за год замен оснований на сайт, а 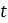 обозначает время в годах, то количество мутаций, которое произойдет в течение этого времени, составляет
обозначает время в годах, то количество мутаций, которое произойдет в течение этого времени, составляет 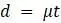 базовых замен на сайт.
базовых замен на сайт.












