Будет стараться нарисовать диаграмму, состоящую из отрезков линий, которая представляет собой эволюционную историю таксонов. Каждый из сегментов линии на диаграмме по устоявшейся в теории графов терминологии называется ребром. Диаграмма, подобная приведенной выше, в которой нет циклов и петель, образованных ребрами, называется деревом.
Вопросы для самопроверки:
– Почему разумно предположить, что эволюционные отношения могут быть смоделированы путем рисования именно деревьев? Что бы это значило, если бы существовали цикл или петля?
Поскольку существует боковой перенос генов, например, когда вирусная ДНК постоянно включается в ДНК хозяина, деревья не могут описать все эволюционные отношения. Они обеспечивают простейшую модель, которая, тем не менее, полностью адекватна для большинства применений.
Точка, в которой сходятся нескольких ребер называется внутренней вершиной, в то время как висячий конец ребра у таксона называется конечной вершиной или листом дерева. Вершина, в которой будет находиться общий предок всех таксонов, называется корнем.
Говорят, что дерево раздваивается, находится в состоянии бифуркации, если на каждой его внутренней вершине встречаются по три ребра, а у корня сходится два ребра, как на деревьях на рисунке 5.1. Такие деревья называют двоичными или бинарными. Хотя с биологической точки зрения возможно, что дерево, отличное от двоичного, могло бы описывать эволюционную историю, обычно эту возможность игнорируют.
Вопросы для самопроверки:
– Каково было бы эволюционное значение вершины в дереве, где встречаются четыре ребра (то есть, где маршрут из одного ребра расходится на три направления)? Можете ли представить себе правдоподобные обстоятельства, при которых несколько видов могут расходиться таким образом?
Хотя в идеале каждое филогенетическое дерево должно иметь корень, показывающий общего предка таксонов, иногда приходится обходиться без него. Некоторые методы филогенетического построения деревьев дают некорневые деревья. Например, на рисунке 5.2 показано некорневое дерево и несколько корневых деревьев, которые с ним согласуются. Два дерева справа могли быть согнуты и растянуты, чтобы выглядеть как дерево слева; их отличает только расположение корня.
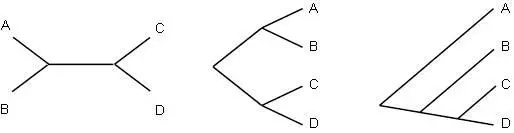
Рисунок 5.2. Некорневое дерево (слева) и две его корневые версии (в центра и справа).
Посмотрим на деревья с топологической точки зрения. Дерево, относящееся к ряду таксонов, может фактически указывать несколько различных типов информации об их отношениях. Во-первых, если не указываем длины ребер, а значит, смотрим только на ветвящуюся структуру, то рассматриваем только топологию дерева. Считается, что два дерева топологически одинаковы, если можно согнуть и растянуть ребра одного из них, чтобы получить второе дерево. Однако нельзя отрезать ребро и снова прикреплять его в другом месте; это может дать дерево, которое топологически отличается от исходного.
На рисунке 5.3 деревья 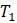 ,
, 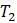 и
и 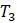 топологически совпадают с некорневыми деревьями, потому что, если бы какая-либо из этих фигур была сделана из резины, ее можно было бы деформировать в другие, не разрезая и не склеивая куски вместе. Дерево
топологически совпадают с некорневыми деревьями, потому что, если бы какая-либо из этих фигур была сделана из резины, ее можно было бы деформировать в другие, не разрезая и не склеивая куски вместе. Дерево 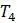 , напротив, топологически отличается от
, напротив, топологически отличается от 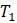 ,
, 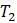 и
и 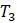 .
.
Для корневых деревьев используем аналогичную концепцию. Два корневых дерева топологически эквивалентны, если одно можно преобразовать в другое, не перемещая корень. Можно изменить длину ребер, но не структуру ветвления.
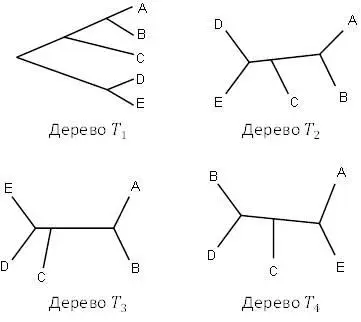
Рисунок 5.3. Четыре топологических дерева; как некорневые деревья, все, кроме правого нижнего, они идентичны.
Вопросы для самопроверки:
– Как на рисунке 5.3 расположить корень дерева 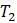 , чтобы полученное дерево не было топологически эквивалентным корневому дереву
, чтобы полученное дерево не было топологически эквивалентным корневому дереву 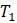 ? А чтобы получилось топологически то же самое, что и корневое дерево
? А чтобы получилось топологически то же самое, что и корневое дерево 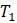 ?
?
Читать дальше


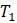 ,
, 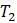 и
и 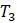 топологически совпадают с некорневыми деревьями, потому что, если бы какая-либо из этих фигур была сделана из резины, ее можно было бы деформировать в другие, не разрезая и не склеивая куски вместе. Дерево
топологически совпадают с некорневыми деревьями, потому что, если бы какая-либо из этих фигур была сделана из резины, ее можно было бы деформировать в другие, не разрезая и не склеивая куски вместе. Дерево 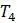 , напротив, топологически отличается от
, напротив, топологически отличается от 











