Эндрю Уэзеролл - Компьютерные сети. 5-е издание

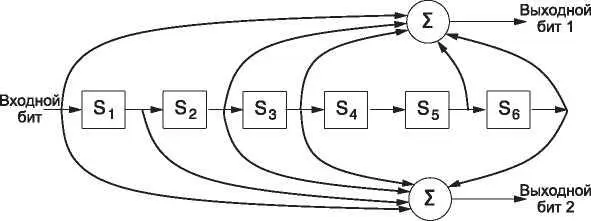
Рис. 3.7.Двоичный сверточный код NASA применяется в сетях 802.11

Внутреннее состояние хранится в шести регистрах памяти. При поступлении на вход очередного бита значения в регистрах сдвигаются вправо. Например, если на вход подается последовательность 111, а в первоначальном состоянии в памяти только нули, то после подачи первого, второго и третьего бита оно будет меняться на 100000, 110000 и 111000 соответственно. На выходе получатся значения 11, затем 10 и затем

01. Для того чтобы полностью подавить первоначальное состояние регистров (тогда оно не будет влиять на результат), требуется семь сдвигов. Длина кодового ограничения для данного кода k, таким образом, равна 7.

Декодирование сверточного кода осуществляется путем поиска последовательности входных битов, с наибольшей вероятностью породившей наблюдаемую последовательность выходных битов (включающую любые ошибки). Для небольших значений k это делается с помощью широко распространенного алгоритма, разработанного Витерби (Forney, 1973). Этот алгоритм проходит по наблюдаемой последовательности, сохраняя для каждого шага и для каждого возможного внутреннего состояния входную последовательность, которая породила бы наблюдаемую последовательность с минимальным числом ошибок. Входная последовательность, которой соответствует минимальное число ошибок, и есть наиболее вероятное исходное сообщение.

Сверточные коды были очень популярны для практического применения, так как в декодировании очень легко учесть неопределенность значения бита (0 или 1). Например, предположим, что -1 В соответствует логическому уровню 0, а +1 В соответствует логическому уровню 1. Мы получили для двух бит значения 0,9 В и -0,1 В. Вместо того чтобы сразу определять соответствие — 1 для первого бита и 0 для второго, — можно принять 0,9 В за «очень вероятную единицу», а -0,1 В за «возможный нуль» и скорректировать всю последовательность. Для более надежного исправления ошибок к неопределенностям можно применять различные расширения алгоритма Витерби. Такой подход к обработке неопределенности значения бит называется декодированием с мягким принятием решений( soft-decision decoding). И наоборот, если мы решаем, какой бит равен нулю, а какой единице, до последующего исправления ошибок, то такой метод называется декодированием с жестким принятием решений ( hard-decision decoding).

Третий тип кода с исправлением ошибок, с которым мы познакомимся, называется кодом Рида—Соломона. Как и коды Хэмминга, коды Рида—Соломона относятся к линейным блочным кодам; также многие из них систематические. Но в отличие от кодов Хэмминга, которые применяются к отдельным битам, коды Рида—Соломона работают на группах из m-битовых символов. Разумеется, математика здесь намного сложнее, так что применим аналогию.

Коды Рида-Соломона основываются на том факте, что каждый многочлен п-й степени уникальным образом определяется п + 1 точкой. Например, если линия задается формулой ax + b, то восстановить ее можно по двум точкам. Дополнительные точки, лежащие на той же линии, излишни, но они полезны для исправления ошибок. Предположим, что две точки данных представляют линию. Мы отправляем по сети эти две точки данных, а также еще две контрольные точки, лежащие на той же линии. Если в значение одной из точек по пути закрадывается ошибка, то точки данных все равно можно восстановить, подогнав линию к полученным правильным точкам. Три точки окажутся на линии, а одна, ошибочная, будет лежать вне ее. Обнаружив правильное положение линии, мы исправили ошибку.

В действительности, коды Рида—Соломона определяются как многочлены на конечных полях. Для m-битовых символов длина кодового слова составляет 2 m- 1 символов. Очень часто выбирают значение m = 8, то есть одному символу соответствует один байт. Тогда длина кодового слова — 255 байт. Широко используется код (255,233), он добавляет 32 дополнительных символа к 233 символам данных. Декодирование с исправлением ошибок выполняется при помощи алгоритма, разработанного Берлекэмпом и Мэсси, который эффективно осуществляет подгонку для кодов средней длины (Massey, 1969).

Коды Рида—Соломона широко применяются на практике благодаря хорошим возможностям по исправлению ошибок, особенно последовательных. Они используются в сетях DSL, в кабельных и спутниковых сетях, а также для исправления ошибок на компакт-дисках, дисках DVD и Blu-ray. Поскольку работа идет на базе m-битных символов, однобитные ошибки и m-битные последовательные ошибки обрабатываются одинаково — как одна символьная ошибка. При добавлении 2t избыточных символов код Рида—Соломона способен исправить до t ошибок в любом из переданных символов. Это означает, например, что код (255,233) с 32 избыточными символами исправляет до 16 символьных ошибок. Так как символы могут быть последовательными, а размер их обычно составляет 8 бит, то возможно исправление последовательных ошибок в 128 битах. Ситуация выглядит еще лучше, если модель ошибок связана с удалением данных (например, царапина на компакт-диске, уничтожившая несколько символов). В таком случае возможно исправление до 2t ошибок.