Эндрю Уэзеролл - Компьютерные сети. 5-е издание

При заданном m данная формула описывает нижний предел требуемого количества контрольных бит для возможности исправления одиночных ошибок.

Этот теоретический нижний предел может быть достигнут на практике с помощью метода Хэмминга (1950). В кодах Хэмминга биты кодового слова нумеруются последовательно слева направо, начиная с 1. Биты с номерами, равными степеням 2 (1, 2, 4, 8, 16 и т. д.), являются контрольными. Остальные биты (3, 5, 6, 7, 9, 10 и т. д.) заполняются m битами данных. Такой шаблон для кода Хэмминга (11,7) с 7 битами данных и 4 контрольными битами показан на рис. 3.6. Каждый контрольный бит обеспечивает сумму по модулю 2 или четность некоторой группы бит, включая себя самого. Один бит может входить в несколько вычислений контрольных бит. Чтобы определить, в какие группы контрольных сумм будет входить бит данных в k-й позиции, следует разложить k по степеням числа 2. Например, 11 = 8 + 2 + 1, а 29 = 16 + 8 + 4 + 1. Каждый бит проверяется только теми контрольными битами, номера которых входят в этот ряд разложения (например, 11-й бит проверяется битами 1, 2 и 8). В нашем примере контрольные биты вычисляются для проверки на четность в сообщении, представляющем букву «A» в кодах ASCII.

Расстояние этого кода равно 3, то есть он позволяет исправлять одиночные ошибки (или распознавать двойные). Причина такой сложной нумерации бит данных и контрольных бит становится очевидной, если рассмотреть процесс декодирования. Когда

прибывает кодовое слово, приемник повторяет вычисление контрольных бит, учитывая значения полученных контрольных бит. Их называют результатами проверки. Если контрольные биты правильные, то для четных сумм все результаты проверки должны быть равны нулю. В таком случае кодовое слово принимается как правильное.

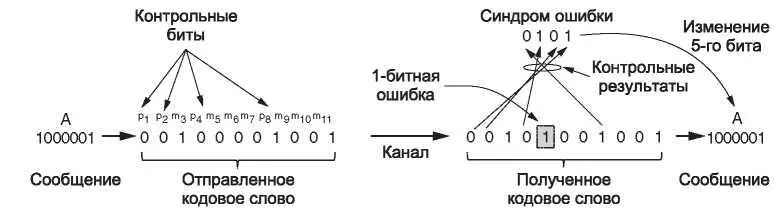
Рис. 3.6. Пример кода Хэмминга (11,7), исправляющего однобитную ошибку

Если не все результаты проверки равны нулю, это означает, что обнаружена ошибка. Набор результатов проверки формирует синдром ошибки( error syndrome), с помощью которого выделяется и исправляется ошибка. На рис. 3.6 в канале произошла ошибка в одном бите. Результаты проверки равны 0, 1, 0 и 1 для k = 8, 4, 2 и 1 соответственно. Таким образом, синдром равен 0101 или 4 + 1 = 5. Согласно схеме, пятый бит содержит ошибку. Поменяв его значение (а это может быть контрольный бит или бит данных) и отбросив контрольные биты, мы получим правильное сообщение: букву «A» в кодах ASCII.

Кодовые расстояния полезны для понимания блочных кодов, а коды Хэмминга применяются в самокорректирующейся памяти. Однако в большинстве сетей используются более надежные коды. Второй тип кода, с которым мы познакомимся, называется сверточным кодом. Из всех рассмотренных в данной книге только он не относится к блочному типу. Кодировщик обрабатывает последовательность входных бит и генерирует последовательность выходных бит. В отличие от блочного кода, никакие ограничения на размер сообщения не накладываются, также не существует грани кодирования. Значение выходного бита зависит от значения текущего и предыдущих входных бит — если у кодировщика есть возможность использовать память. Число предыдущих бит, от которого зависит выход, называется длиной кодового ограничения для данного кода. Сверточные коды описываются в терминах кодовой нормы и длины кодового ограничения.

Сверточные коды широко применяются в развернутых сетях. Например, входят в мобильную телефонную систему GSM, спутниковые сети и сети 802.11. В качестве примера можно рассмотреть популярный сверточный код, показанный на рис. 3.7. Он называется сверточным кодом NASA с r = 1/2 и k = 7 (впервые этот код был использован при подготовке космического полета станции Voyager, запущенной в 1977 году). С тех пор он постоянно используется в других приложениях, таких как сети 802.11.

На рис. 3.7 для каждого входного бита слева создается два выходных бита справа. Эти выходные биты получаются путем применения операции исключающего ИЛИ к входному биту и внутреннему состоянию. Так как кодирование работает на уровне бит и использует линейные операции, это двоичный линейный сверточный код. Поскольку один входной бит создает два выходных бита, кодовая норма r равна 1/2. Этот код не систематический, так как входные биты никогда не передаются на выход напрямую, без изменений.