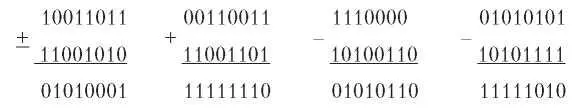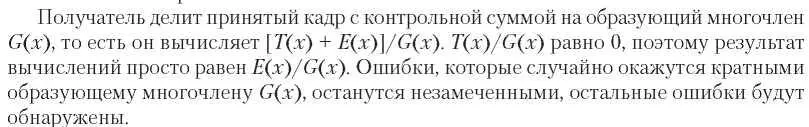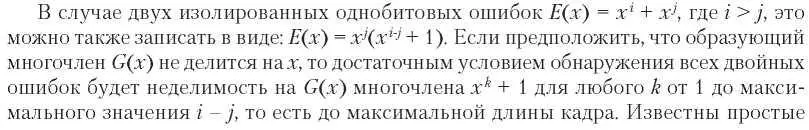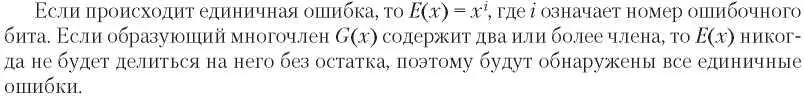Эндрю Уэзеролл - Компьютерные сети. 5-е издание

ной суммы. В противном случае при сложении двух старших бит переполнение может быть утеряно без изменения суммы. Но есть и еще одно преимущество. У дополнения до единицы может быть два представления нуля: все нули и все единицы. Таким образом, одно значение (например, все нули) указывает, что контрольной суммы нет и дополнительное поле для этого не требуется.

Десятилетиями существовало мнение, что кадры, для которых вычисляется контрольная сумма, содержат случайные значения бит. Анализ алгоритмов вычисления контрольных сумм всегда проводился с учетом именно такого предположения. Изучение фактических данных, выполненное Партриджем и другими в 1995 году, показало, что данное предположение неверно. Следовательно, нераспознанные ошибки проскальзывают в некоторых случаях намного чаще, чем полагали раньше.

В частности, контрольная сумма для Интернета, несмотря на эффективность и простоту, в определенных ситуациях слабо защищает от ошибок именно потому, что это простая сумма. Она не позволяет распознать удаление или добавление нулевых данных, а также случаи, когда части сообщения меняются местами или расщепляются таким образом, что склеенными оказываются части двух разных пакетов. Может казаться, что подобные ошибки вряд ли произойдут в случайных процессах, но они вполне вероятны в сетях с неправильно работающим оборудованием.

Намного лучшим выбором считается контрольная сумма Флетчера (Fletcher, 1982). Она включает компонент, отвечающий за позицию: произведение значения данных и соответствующей позиции добавляется к текущей сумме. Это обеспечивает лучшие возможности по обнаружению изменений в положении данных.

Хотя две приведенные выше схемы в некоторых случаях могут быть приемлемыми на более высоких уровнях, на практике на канальном уровне широко используется другой, более надежный метод обнаружения ошибок — полиномиальный код, так же известный, как CRC (Cyclic Redundancy Check — циклический избыточный код).

С данными многочленами осуществляются арифметические действия по модулю 2 в соответствии с алгебраической теорией поля. При этом перенос при сложении и заем при вычитании не производится. И сложение, и вычитание эквивалентны исключающему ИЛИ (XOR).

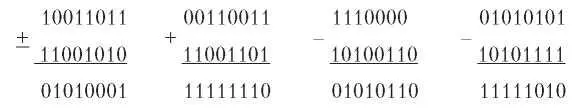
Деление чисел осуществляется в точности так же, как и деление обычных двоичных чисел, с той разницей, что вычитание производится снова по модулю 2. Говорят, что делитель «уходит» в делимое, если в делимом столько же бит, сколько в делителе.

При использовании циклического кода отправитель и получатель должны сначала договориться насчет образующего многочлена, G(x). Старший и младший биты образующего многочлена должны быть равны 1. Для вычисления CRC для некоторого кадра из m бит, соответствующего полиному M(x), необходимо, чтобы этот кадр был длиннее образующего многочлена. Идея состоит в добавлении CRC в конец кадра таким образом, чтобы получившийся многочлен делился на образующийся многочлен G ( x ) без остатка. Получатель, приняв кадр, содержащий контрольную сумму, пытается разделить его на G(x). Ненулевой остаток от деления означает ошибку.

Должно быть очевидно, что многочлен T(x) делится (по модулю 2) на G(x) без остатка. В любом случае, если вы уменьшите делимое на остаток, то результат должен делиться без остатка. Например, в десятичной системе счисления, если разделить 210 278 на 10 941, то остаток от деления будет равен 2399. Если вычесть 2399 из 210 278, то результат (207 879) будет делиться на 10 941 без остатка.

Теперь проанализируем возможности этого метода. Какие ошибки сможет он обнаруживать? Представим, что произошла ошибка при передаче кадра, так что вместо многочлена T(x) получатель принял T(x) + E(x). Каждый единичный бит многочлена E(x) соответствует инвертированному биту в пакете. Если в многочлене E(x) k бит равны 1, это означает, что произошло k единичных ошибок. Единичный пакет ошибок характеризуется первой единицей, смесью нулей и единиц и конечной единицей, а остальные биты равны 0.