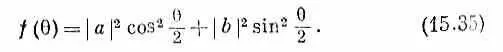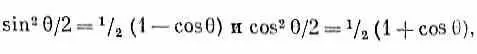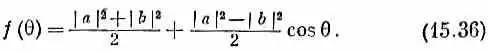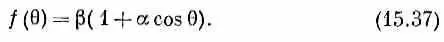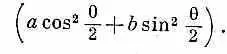Feynmann - Feynmann 9

Те два процесса, к которым относятся эти амплитуды, показаны

на фиг. 15.9.

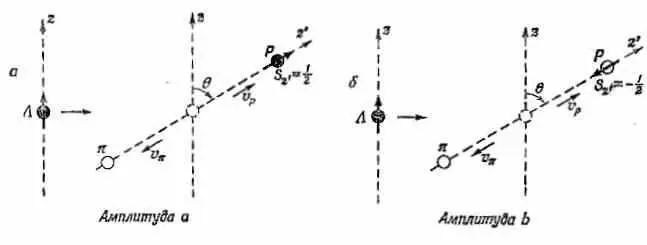
Фиг . 15.9. Два возможных состояния распада L 0 .

Теперь зададим такой немудреный вопрос. Пусть мы соби­раемся регистрировать протоны, вылетающие под углом q, не интересуясь их спином. Два спиновых состояния (вверх и вниз по оси z') различимы, даже если бы мы того и не хотели. Значит, чтобы получить вероятность, надо амплитуды возвысить в квад­рат и сложить. Вероятность f (q) обнаружить протон в неболь­шом телесном угле qW при q равна

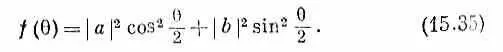
Вспоминая, что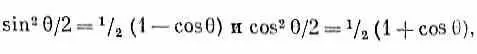

запишем f (q) так:

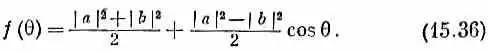
Угловое распределение имеет вид

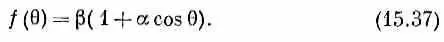
Одна часть вероятности не зависит от q, а другая зависит от cosq линейно. Из измерений углового распределения мы можем получить a и b, а значит, и | а | , и | b | .

Можно получить ответ и на многие другие вопросы. Может быть, вас интересуют лишь те протоны, спин которых направлен вверх относительно старой оси z? Каждый член в (15.33) и (15.34) даст амплитуду того, что спин протона окажется направ­ленным вверх или вниз по отношению к оси z ' (|+ z '> и |- z '>). А состояние, когда спин направлен вверх относитель­но старой оси, | + z), можно выразить через два базисных со­стояния | + z ' > и |-z'>. Можно тогда взять две амплитуды (15.33) и (15.34) с надлежащими коэффициентами (cosq/2 и -sinq/2) и получить полную амплитуду

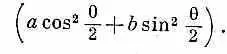
Ее квадрат даст вероятность того, что протон вылетит под углом q со спином, направленным туда же, куда направлен спин L 0(вверх по оси z ).

Если бы четность сохранялась, можно было бы сделать еще одно утверждение. Распад на фиг. 15.8 — это просто зеркальное отражение, скажем в плоскости yz , распада с фиг. 15.7. Если бы четность сохранялась, b равнялось бы либо a , либо - а . Тогда коэффициента в (15.37) был бы равен нулю и распад оди­наково часто происходил бы во всех направлениях.

Результаты опытов говорят, однако, что при распаде асим­метрия существует. Измеренное угловое распределение дейст­вительно, как мы предсказали, меняется по закону cosq, а не по закону cos 2q или по другой степени. Из этого углового распределения, стало быть, следует, что спин L 0равен 1/ 2 . Кроме того, мы видим, что четность не сохраняется. Действи­тельно, коэффициента на опыте найден равным -0,62±0,05, так что b примерно вдвое больше а. Отсутствие симметрии от­носительно отражений совершенно очевидно.

Вы видите, как много можно вывести из сохранения момента количества движения. Еще некоторые примеры будут приведены в следующей главе.

· · ·

Замечание после лекции. Под амплитудой а здесь мы подразумевали амплитуду того, что состояние

| протон летит по + z, спин по + z> обра­зовано за бесконечно малое время dt из состояния |L, спин по + z>, или, иными словами, что

<���протон летит по + z , спин по +z| H |L, спин по + z>= iha , (15.38)

где H — гамильтониан всего мира или по крайней мере той его части, которая ответственна за L-распад. Сохранение момента количества дви­жения означает, что у гамильтониана должно быть такое свойство:

<���протон летит по +z, спин по -z| H |L, спин по +z>=0. (15.39)

Под амплитудой b подразумевается, что

<���протон летит по + z, спин по —z| H |L, спин по -z>= ihb . (15.40)

Сохранение момента количества движения предполагает, что

<���протон летит по + z, спин по + z | H |L , спин по -z>=0. (15.41)

Если вам не ясно, как написаны амплитуды (15.33) и (15.34), можно их записать в более математической форме. Когда мы писали (15.33), нам нужна была амплитуда того, что Л со спином, направленным по +z, распадается на протон, движущийся вдоль направления + z ' и обладаю­щий спином, направленным тоже по + z ', т. е.