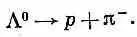Feynmann - Feynmann 9

Мы говорили, что частица со спином 1 может иметь три зна­чения J z : +1, 0, -1 (те три состояния, которые нам встрети­лись в опыте Штерна — Герлаха).

Но у света свой нрав: у него только два состояния. Состоя­ния с нулем у него нет. Эта странная потеря связана с тем, что свет не может стоять на месте. У покоящейся частицы со спином j имеются 2 j +1 возможных состояния со значениями j z , идущими с шагом 1 от - j до + j . Но оказывается, что если что-то имеет спин j , а масса этого чего-то равна нулю, то у него могут быть только состояния с компонентами + j и - j вдоль направ­ления движения. Например, у света не три состояния, а два, хотя фотон — это объект со спином 1. Как же это согласуется с нашими прежними доказательствами, опирающимися на то, что происходит при поворотах в пространстве, доказательства­ми того, что для частиц со спином 1 необходима тройка состоя­ний? Покоящуюся частицу можно поворачивать вокруг любой оси, не меняя состояния ее момента. Частицы же с нулевой массой покоя (например, фотоны или нейтрино) не могут на­ходиться в покое; только повороты вокруг оси, указывающей направление движения, не изменят состояния момента. А пово­ротов вокруг одной оси не хватает на то, чтобы доказать, что нужны обязательно три состояния, если дано, что одно из них при поворотах на угол j меняется, как е i j .

Еще одно замечание в сторону. Вообще-то частицы с нулевой массой покоя могут обойтись только одним из двух спиновых со­стояний (+ j , - j ) относительно линии движения. У нейтрино (частиц со спином 1/ 2) в природе существуют только состояния с компонентой момента количества движения - h /2, обратной направлению движения (а у антинейтрино — только с компо­нентой по направлению движения, + h /2). Когда же система обладает симметрией инверсии (так что четность сохраняется), требуются уже обе компоненты + j и - j . Примером является свет.

§ 5 . Распад L 0

Теперь приведем пример того, как теорема о сохранении мо­мента количества движения применяется в чисто квантовофизических задачах. Рассмотрим распад лямбда-частицы (L 0), кото­рая расщепляется на протон и p --мезон посредством слабого взаимодействия:

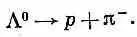
Пусть нам известно, что спин у пиона равен нулю, у протона — половине, а у L 0тоже половине. Мы хотели бы решить следую­щую задачу: положим, что L 0рождена таким образом, что ока­залась полностью поляризованной; это значит, что ее спин направлен, скажем, вверх по отношению к подходящим образом выбранной оси z (фиг. 15.6, а).

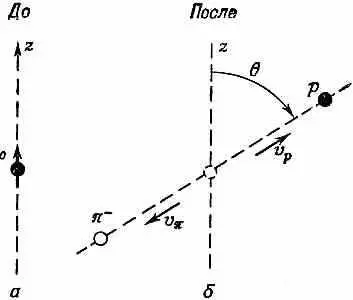
Фиг. 15.6. L 0 -частица со спином, направленным вверх, распадается на протон и пион (в системе центра масс).

Какова вероятность того, что протон вылетит под углом q ?

Вопрос заключается в том, с какой вероятностью она распадется так, что протон вылетит под углом q к оси z (фиг. 15.6, б). Иными словами, каково угло­вое распределение распадов? Мы будем рассматривать распад в системе координат, где L 0покоится, измеряя углы в системе покоя L 0; если нужно, их всегда можно перевести в другую

систему.

Начнем с рассмотрения того частного случая, когда протон испускается в небольшой телесный угол DW близ оси z (фиг. 15.7).

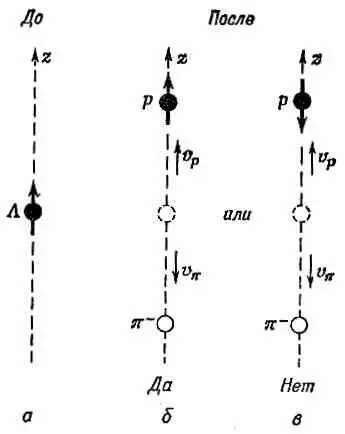
Фиг. 15.7. Две возможности распада частицы L 0 со спином, направленным вверх, если про­тон движется по оси +z.

Момент сохраняется только при схеме распада (б).

До распада спин L 0был направлен вверх (фиг. 15.7, а). Через мгновение (по причинам, по сей день неизвестным, известно только, что они связаны со слабыми распадами) L 0взрывается, образуя протон и пион. Пусть протон летит вверх по оси + z. Тогда пиону из-за сохранения импульса придется направиться вниз. Поскольку протон — это частица со спином 1/ 2, то его спин обязан быть направлен либо вверх, либо вниз,— в принципе имеются две возможности, показанные на фиг. 15.7, б и в . Со­хранение момента количества движения требует, однако, чтобы спин протона был направлен только вверх. Легче всего понять это из следующих рассуждений. Частица, движущаяся вдоль оси z , никак не может приобрести за счет своего движения момента вокруг этой оси, поэтому в J z могут дать вклад только спины. Спиновый момент количества движения вокруг оси z до распада был равен + h /2; значит, и после он будет равен + h /2 . Можно сказать, что из-за того, что у пиона нет спина, спин протона должен смотреть вверх.