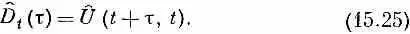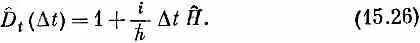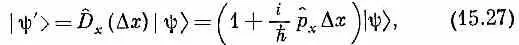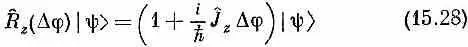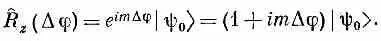Feynmann - Feynmann 9

Чтобы вы смогли разобраться в других книгах по кванто­вой механике, мы сделаем небольшую техническую ремарку и познакомим вас с одним общепринятым обозначением. Операция сдвига по времени — это как раз та самая операция U ^, о кото­рой мы как-то говорили:

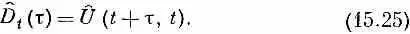
Многие предпочитают язык бесконечно малых сдвигов по времени или бесконечно малых перемещений в пространстве или пово­ротов на бесконечно малые углы. Поскольку всякое конечное смещение или угол можно постепенно накопить последователь­ными бесконечно малыми смещениями или поворотами, то часто легче проанализировать сначала этот бесконечно малый случай. Оператор бесконечно малого сдвига D t во времени есть (по определению гл. 6, вып. 8)

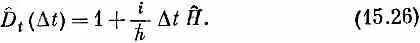
Тогда Н аналогично классической величине, которую мы име­нуем энергией, потому что если Н ^ |y> оказывается равным

постоянной, умноженной на |y>, а именно если Н ^ |y>= E |y>,

то эта постоянная есть энергия системы.

То же самое проделывается и с другими операциями. Если мы делаем легкое смещение по х, скажем на D x , то состояние

|y>, вообще говоря, перейдет в некоторое новое состояние

|y'>. Мы можем написать

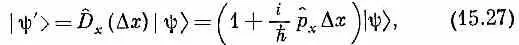
потому что, когда D x стремится к нулю, |y'> обязано обратиться опять в |y>, или, что то же самое, D ^ x (0)=1, а для малых D x отклонение D ^ x (D x ) от единицы должно быть пропорционально D x . Оператор р х , определенный таким путем, называется оператором импульса (естественно, для x -компоненты).

По тем же причинам для малых поворотов обычно пишут

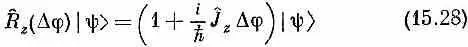
и называют J ^ zоператором z -компоненты момента количества движения. Для тех особых состояний, для которых R ^ z (j)|y 0>=е im j|y 0>, можно для каждого малого угла, скажем Dj, разложить правую часть до членов первого порядка по Dj и получить

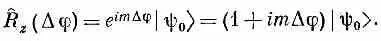
Сравнивая это с определением J ^ z по формуле (15.28), приходим к

Иначе говоря, если вы действуете оператором J ^ z на состояние с определенным моментом количества движения вокруг оси z, то получаете mh , умноженное на это состояние, где mh — коли­чество z-компоненты момента количества движения. Все совер­шенно аналогично тому, как действие Н ^ на состояние с опреде­ленной энергией дает Е |y>.

Теперь хотелось бы перейти к некоторым приложениям идеи о сохранении момента количества движения, чтобы показать вам ее в действии. Дело в том, что в действительности все это очень просто. О том, что момент количества движения сохраняется, вы знали и раньше. Единственное, что вам нужно запомнить из этой главы, это что если у состояния |y 0> есть такое свойство, что при повороте на угол j вокруг оси z оно превращается в е im j |y 0>, то z-компонента момента количества движения равна mh . Этих знаний достаточно, чтобы получить уйму инте­ресных вещей.

§ 4. Поляризованный свет

Прежде всего необходимо проверить одну идею. В гл. 9, § 4 (вып. 8), мы показали, что когда состояние правополяризованного по кругу света наблюдается из системы, повернутой на угол j вокруг оси z, то оно оказывается умноженным на е i j . Не означает ли это, что фотоны правополяризованного по кругу света несут момент количества движения вдоль оси z, равный единице?

Да, так оно и есть. Это означает еще, что когда у нас имеется пучок света, содержащий множество фотонов, поголовно оди­наково поляризованных по кругу (как бывает в классических пучках), то он будет нести с собой какой-то момент количества движения. Если полная энергия, уносимая пучком за какое-то время, есть W , то в нем имеется N = W /hw фотонов. Каждый несет по моменту h , так что полный момент количества движения равен