Feynmann - Feynmann 9

Мы знаем, что если |y 0> — состояние определенной энергии, то

где Е — просто число, энергия состояния. Если у нас имеется произвольный оператор Q ^, который является оператором сим­метрии для системы, то мы можем доказать, что

если только |y 0> — единственное состояние с данной энергией. Рассмотрим новое состояние |y 0> которое вы получаете после действия Q ^. Если вся физика симметрична, то |y' 0> должно иметь ту же энергию, что и |y 0>. Но мы ведь выбрали случай, когда состояние с такой энергией только одно, а именно |y 0>; значит, |y' 0> должно быть тем же состоянием, отличаясь разве что фазой. Таково физическое доказательство.

Но то же последует и из нашей математики. Наше определе­ние симметрии —это (15.10) или (15.11), справедливое для лю­бого состояния |y>:

Но сейчас речь идет о состоянии |y 0>, которое является состоя­нием с определенной энергией, так что Н ^ |y 0>= Е |y 0>. А раз Е — просто число, то оно попросту проходит сквозь Q ^, и мы имеем

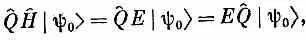
так что

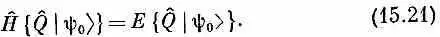
Значит, |y' 0>= Q ^ ly 0> — тоже состояние H ^ с определенной энергией и при этом с тем же самым Е. Но по нашей гипотезе имеется только одно такое состояние; значит, |y 0> должно быть равно ё i d |y 0>.

Все, что мы только что доказали, относится к любому опера­тору Q ^, лишь бы он был оператором симметрии для физической системы. Поэтому когда в рассмотрение входят только электрические силы и сильные взаимодействия (и нет никакого b-распада), так что симметрия относительно инверсии является вполне допустимым приближением, в этих обстоятельствах Р ^ |y>=е i d |y>. Но мы видели также, что е i d обязано равняться либо +1, либо -1. Итак, любое состояние с определенной энергией (если оно не вырождено) навсегда снабжено либо положитель­ной, либо отрицательной четностью.

§ 3. Законы сохранения

Обратимся теперь к другому интересному примеру операции симметрии — к повороту. Рассмотрим частный случай опера­тора, который поворачивает атомную систему на угол j вокруг оси z. Обозначим этот оператор R^z(φ). Предположим еще, что никаких влияний, выстроенных вдоль осей х и у, в нашем физи­ческом случае нет. Все электрические или магнитные поля взяты параллельными оси z, так что никаких изменений во внешних условиях от поворота всей физической системы вокруг оси z не наступит. Например, если имеется атом в пустом простран­стве и мы повернем этот атом вокруг оси z на угол j, то получим ту же физическую систему.

Тогда существуют особые состояния, обладающие тем свойст­вом, что такая операция создает новое состояние, равное перво­начальному, умноженному на некоторый фазовый множитель. Заметим, что когда это так, то изменение фазы обязано быть всегда пропорционально углу j. Представьте, что вы дважды захотели бы сделать поворот на угол j. Это равносильно тому, что повернуть на угол 2j. Если поворот на угол j имеет своим следствием умножение состояния |y 0> на фазовый множи­тель e i d , так что

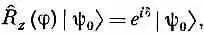
то два таких поворота, один вслед за другим, привели бы к умножению состояния на множитель (е i d ) 2=е i 2 d , так как

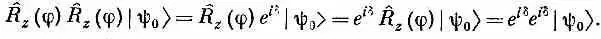
Изменение фазы d оказывается пропорциональным φ. Мы, стало быть, рассматриваем лишь те особые состояния |y 0>, для которых

R^ z(j)|y 0> =e im j |y 0>, (15.22)

где m — некоторое вещественное число.

Нам известен также тот примечательный факт, что если система симметрична относительно поворота вокруг z и если исходное состояние обладает тем свойством, что (15.22) окажется выполненным, то и позже у этого состояния сохранится то же свойство. Значит, это число m имеет большую важность. Если его значение мы знаем в начале, то мы знаем его и в конце. Это число m , которое сохраняется, есть константа движения. Причи­на, почему мы говорим об m , выталкиваем его на первый план, состоит в том, что оно не связано с каким-либо определенным углом j, и еще потому, что у него есть соответствие в классиче­ской механике. В квантовой механике мы выбираем для mh (в состояниях, подобных |y 0>) название момент количества движения вокруг оси z . И тогда мы обнаруживаем, что в пределе больших систем та же величина равняется z-компоненте момента количества движения из классической механики. Значит, если мы имеем состояние, для которого поворот вокруг оси z при­водит просто к фазовому множителю e im j , то перед нами со­стояние с определенным моментом количества движения во­круг этой оси, и момент количества движения сохраняется. Он навсегда остается равным mh . Конечно, повороты можно делать вокруг любых осей, и сохранение момента количества движения тоже будет получаться для любых осей. Вы видите, что сохранение момента количества движения связано с тем фактом, что, когда вы поворачиваете систему, вы получаете опять то же состояние, только с новым фазовым множителем.