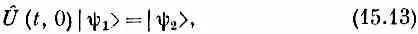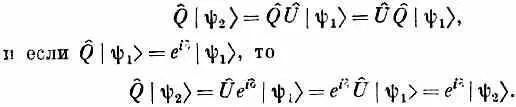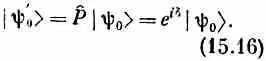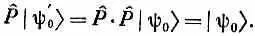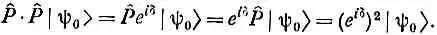Feynmann - Feynmann 9

Далее, ясно, что если оказывается верным, что оператор Q ^ в какой-то момент времени просто меняет фазу состояния (ска­жем, в момент t =0), то это будет верно всегда. Иначе говоря, если состояние |y 1> переходит за время t в состояние |y 2>:

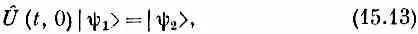
и если симметрия физической картины такова, что

то верно и то, что

Это ясно, ведь

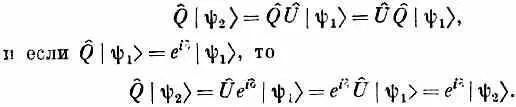
[Верхние равенства следуют из (15.13) и (15.10) для симметричной системы, нижние — из (15.14) и из того, что всякое число, скажем е i d , коммутирует с оператором.]

Итак, при некоторых симметриях то, что верно сначала, вер­но всегда. Но разве это не закон сохранения? Да! Он утверждает, что если вы взглянете на исходное состояние и, проделав где-то в стороне небольшой подсчет, откроете, что операция, которая является операцией симметрии для системы, приводит только к умножению на некоторый фазовый множитель, то вы будете уверены, что это же свойство будет выполнено для конечного состояния — та же операция умножит и конечное состояние на тот же фазовый множитель. Это будет верно всегда, даже если вы ничего не знаете о том внутреннем механизме мира, который изменяет систему от начального состояния к конечному. Даже если вы не позаботились вглядеться в детали того, каким именно способом система переходит от одного состояния к другому, вы все равно имеете право говорить, что если вещь вначале находилась в состоянии с определенным характером симметрии и если гамильтониан этой вещи симметричен отно­сительно этой операции симметрии, тогда тот же характер симметрии останется у состояния на вечные времена. Это основа всех законов сохранения квантовой механики.

Рассмотрим частный пример. Возьмем опять оператор Р ^ . Сперва, правда, немножко изменим определение операции Р. Пусть Р ^ будет не просто зеркальным отражением, потому что оно требует определения плоскости, в которой поставлено зер­кало. Существует особый вид отражения, который указания плоскости не требует. Переопределим операцию Р ^ таким обра­зом: сперва вы отражаете в зеркале, находящемся в плоскости z, так что z переходит в - z , x остается х, а у остается у; затем вы поворачиваете систему на угол 180° вокруг оси z, так что х переходит в - х, а у в - у. Все вместе называется инверсией, обращением координат. Каждая точка проецируется через начало координат в диаметрально противоположное положение. Все координаты всего на свете меняют знак. Эту операцию мы, как и прежде, будем обозначать символом Р. Она изображена на фиг. 15.4 и немного удобнее, чем простая операция отражения, потому что не нужно указывать, в какой координатной плоско­сти происходит отражение, достаточно лишь указать точ­ку, являющуюся центром симметрии.

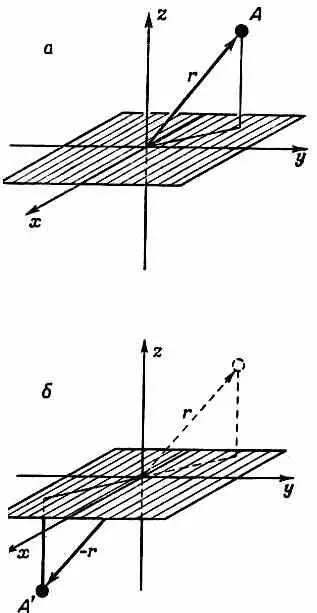
Фиг. 15.4. Операция инверсии Р ^ . То, что находится в точке A (х, у, z), переходит в точку

А' ( - х, - у, - z ).

Теперь предположим, что у sac есть состояние | y 0> , которое при операции инверсии переходит в е i d|y 0>, т. е.

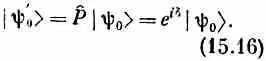
Сделаем теперь новую инверсию. После двух инверсий мы вернемся к тому, с чего начали: ничего не изменится. Должно получиться

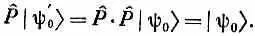
Но

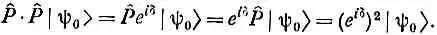
Отсюда следует, что (е i d ) 2=1. Значит, если оператор инверсии является операцией симметрии для какого-то состояния, то У d могут быть только две возможности: