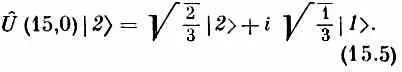Теперь мы хотели бы кое на что обратить ваше внимание. Предположим, что физика всей системы молекулярного иона водорода сама по себе симметрична. Этого могло бы и не быть — это зависит, например, от того, что находится с нею рядом. Но если система симметрична, то с необходимостью должна быть справедлива следующая идея. Предположим, что вначале, при t = 0 , система находится в состоянии | 1 >, а через промежуток времени t мы обнаруживаем, что система оказалась в более сложном положении — в какой-то линейной комбинации обоих базисных состояний. Вспомните, что в гл. 6 (вып. 8) мы привыкли представлять «эволюцию во времени» умножением на оператор U ^. Это означает, что система через мгновение (скажем для определенности, через 15 сек) окажется в каком-то ином состоянии.
Например, это состояние на Ц 2/ 3может состоять из состояния | 1 > и на i Ц 1/ 3из состояния | 2 >, и мы бы написали
|y на 15-й секунде> = 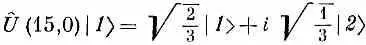 .(15.4)
.(15.4)
Теперь спросим: что же произойдет, если вначале мы запустим систему в симметричном состоянии | 2 > и при тех же условиях подождем 15 сек? Ясно, что если мир симметричен (что мы и предполагаем), то обязательно получится состояние, симметричное с (15.4):
|y на 15-й секунде>= 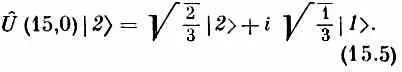
Те же идеи схематично изображены на фиг. 15.2.
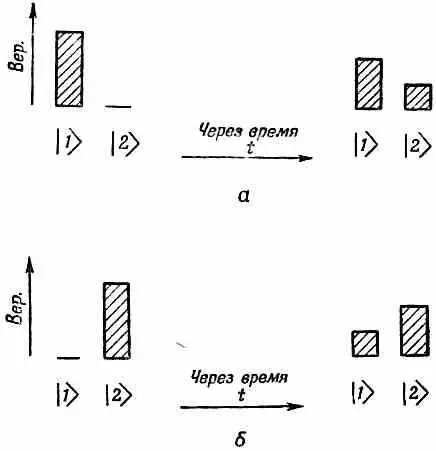
Фиг. 15.2. Если в симметричной системе чистое состояние |1 > развивается во времени так, как показано в части (а), то чистое состояние |2 > будет во времени развиваться так, как показано в части (б).
Итак, если физика системы симметрична относительно некоторой плоскости и мы рассчитали поведение того или иного состояния, то нам также известно поведение состояния, которое получилось бы после отражения исходного состояния в плоскости симметрии.
То же самое можно высказать чуть более общо, т. е. чуть более отвлеченно. Пусть Q ^ — любая из множества операций, которые вы можете произвести над системой, не меняя физики. К примеру, за Q ^ мы можем принять операцию отражения в плоскости, расположенной посредине между двумя атомами молекулы водорода. Или в системе с двумя электронами можно было бы под Q ^ подразумевать операцию обмена двумя электронами. Третьей возможностью явилась бы в сферически симметричной системе операция поворота всей системы на конечный угол вокруг некоторой оси; от этого физика не изменится. Конечно, в каждом отдельном случае мы бы обозначали Q ^ по-своему. В частности, через R ^ y (q) мы обычно будем обозначать операцию «поверни систему вокруг оси у на угол q». Под Q ^ мы просто понимаем один из названных операторов или любой другой, который оставляет всю физическую ситуацию неизменной.
Оператор Q ^ мы будем называть оператором симметрии для системы.
Вот вам еще примеры операторов симметрии. Если у нас имеется атом, а внешнее магнитное или внешнее электрическое поле отсутствует, то после поворота системы координат вокруг любой оси физическая система остается той же самой. Опять-таки молекула аммиака симметрична относительно отражения в плоскости, параллельной той, в которой лежат три атома водорода (пока нет электрического поля). Если есть электрическое поле, то при отражении надо было бы обратить и поле, а это меняет всю физическую задачу. Но пока внешнего поля нет, молекула симметрична.
Теперь рассмотрим общий случай. Положим, мы начали с состояния |y 1>, а через некоторое время или под влиянием других физических условий оно превратилось в состояние |y 2>. Напишем

[Посмотрите на формулу (15.4).] Теперь вообразите, что над всей системой мы проводим операцию Q ^. Состояние |y 1> преобразится в состояние |y' 1>, которое также записывается в виде Q ^ | y 1> . А состояние |y 2> превращается в |y' 2>= Q ^|y 2>. И вот, если физика симметрична относительно Q ^ (не забывайте про это, если это отнюдь не общее свойство системы), тогда, подождав в тех же условиях то же время, мы должны получить
Читать дальше

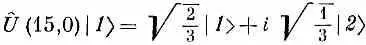 .(15.4)
.(15.4)