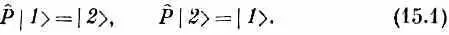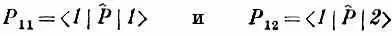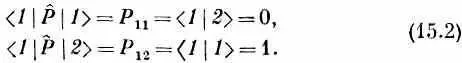Feynmann - Feynmann 9

Глав a 15

СИММЕТРИЯ И ЗАКОНЫ СОХРАНЕНИЯ

§ 1. Симметрия

§ 2. Симметрия и ее сохранение

§ 3. Законы сохранения

§ 4. Поляризованный свет

§ 5. Распад Λ °

§ 6. Сводка матриц поворота

Повторить: гл. 52 (вып. 4} «Сим­метрия законов физики»

§ 1. Симметрия

В классической физике немало величин (та­ких, как импульс, энергия и момент количества движения) сохраняется. Теоремы о сохранении соответствующих величин существуют и в кван­товой механике. Самое прекрасное в квантовой механике это то, что теоремы сохранения в опре­деленном смысле удается в ней вывести из чего-то другого; в классической же механике они сами практически являются исходными для других законов. (Можно, правда, и в классиче­ской механике поступать так же, как в кванто­вой, но это удается только на очень высоком уровне.) В квантовой механике, однако, законы сохранения очень тесно связаны с принципом суперпозиции амплитуд и с симметрией физи­ческих систем относительно различных измене­ний. Это и есть тема настоящей лекции. Хотя идеи эти мы будем применять главным образом к сохранению момента количества движения, но существенно здесь то, что все теоремы о сохранении каких угодно величин всегда связа­ны — в квантовой механике — с симметриями системы.

Начнем поэтому с изучения вопроса о симметриях систем. Очень простым примером слу­жат молекулярные ионы водорода (впрочем, в равной степени подошли бы и молекулы ам­миака), у которых имеется по два состояния. У молекулярного иона водорода за одно базис­ное состояние мы принимали такое состояние, когда электрон расположен возле протона № 1, а за другое базисное со­стояние то, в котором электрон располагался возле протона № 2. Эти два состояния (мы их называли | 1 > и | 2 >) мы снова показываем на фиг. 15.1, а.

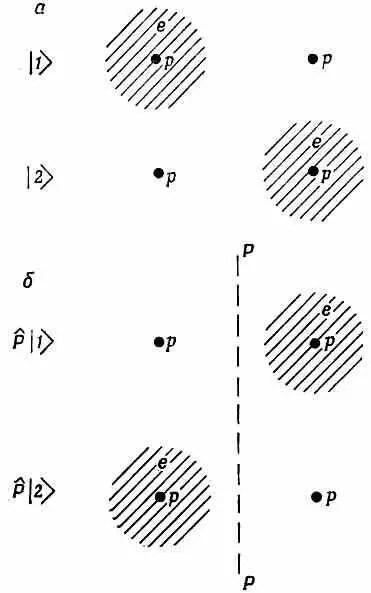
Фиг. 15.1. Если состояния |1 > и |2 > отразить в плоскости Р—Р, они перейдут соответ­ственно в состояния |2> и | 1 >.

И вот, по­скольку оба ядра в точ­ности одинаковы, в этой физической системе име­ется определенная сим­метрия. Иначе сказать, если бы нам пришлось отразить систему в пло­скости, поставленной по­средине между двумя протонами (имеется в виду, если бы все находящееся с одной стороны плоскости симметрично перешло на другую сторону), то возникла бы картина, представленная на фиг. 15.1, б. А коль скоро протоны тождественны, операция отражения пе­реводит | 1 > в | 2 >, а | 2 > в | 1 >. Обозначим эту операцию отражения Р ^ и напишем

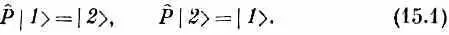
Значит, наше Р ^ — это оператор, в том смысле, что он «что-то делает» с состоянием, чтобы вышло новое состояние. Интересно здесь то, что Р ^ , действуя на любое состояние, создает какое-то другое состояние системы.

Далее, у Р ^ , как у всякого другого оператора, с которыми мы встречались, есть матричные элементы, которые можно определить с помощью обычных очевидных обозначений. Именно

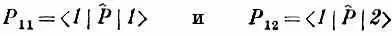
суть матричные элементы, которые получаются, если Р ^ | 1 > и

Р ^ |2 > умножить слева на < 1 | . Согласно уравнению (15.1), они равны

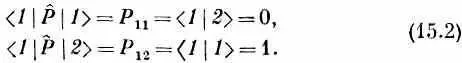
Таким же путем можно получить и Р 21, и Р 22. Матрица Р ^ относительно базисной системы| 1 > и | 2 > есть

Мы снова убеждаемся, что слова оператор и матрица в кван­товой механике практически взаимозаменяемы. Есть, конечно, легкие технические различия, как между словами «числитель­ное» и «число», но мы не такие педанты, чтобы забивать себе этим голову. Так что будем именовать Р ^ то оператором, то мат­рицей, независимо от того, определяет ли оно операцию или реально использовано для получения численной матрицы.