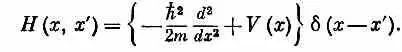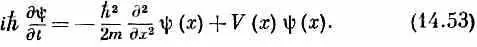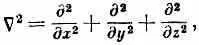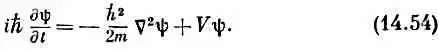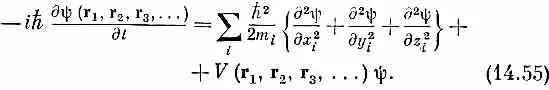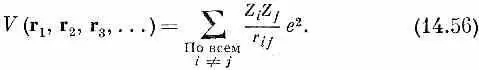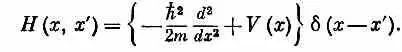
Мы не будем пользоваться этими формулами, а прямо будем работать с (14.52).]
Если теперь взять выражение (14.52) и подставить в (14.50) вместо интеграла, то для y( х ) = < х |y> получится дифференциальное уравнение
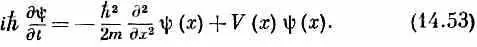
Совершенно очевидно, что надлежит поставить вместо (14.53),
если нас интересует трехмерное движение. Надо только d 2 / dx 2
заменить на
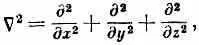
а V ( х ) заменить на V ( x , у, z ) . Для электрона, движущегося в поле с потенциалом V (х, у, z), амплитуда y (х, у, z ) удовлетворяет дифференциальному уравнению
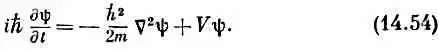
Называется оно уравнением Шредингера и было первым известным квантовомеханическим уравнением. Его написал Шредингер, прежде чем было открыто любое другое описанное в этом томе уравнение.
Хотя мы здесь пришли к нему совсем иным путем, но появление этого уравнения в 1926 г., когда Шредингер впервые его написал, явилось великим историческим моментом, отметившим рождение квантовомеханического описания материи. Многие годы внутренняя атомная структура вещества была великой тайной. Никто не был в состоянии понять, что скрепляет вещество, отчего существует химическая связь, и, особенно, как атомам удается быть устойчивыми. Хотя Бор и смог дать описание внутреннего движения электрона в атоме водорода, которое, казалось бы, объясняло наблюдаемый спектр лучей, испускаемых этим атомом, но причина, отчего электроны движутся именно так, оставалась тайной. Шредингер, открыв истинные уравнения движения электронов в масштабах атома, снабдил нас теорией, которая позволила рассчитать атомные явления количественно, точно и подробно. В принципе его уравнение способно объяснить все атомные явления, кроме тех, которые связаны с магнетизмом и теорией относительности. Оно объясняет уровни энергии атома и все, что касается химической связи. Но, конечно, это объяснение только в принципе. Математика вскоре становится столь сложной, что точно решить удается только простейшие задачи. Одни лишь атомы водорода и гелия были рассчитаны с высокой точностью. Однако путем различных приближений, порой весьма сомнительных, можно многое понять и в более сложных атомах и в химической связи молекул. Некоторые из этих приближений были показаны в предыдущих главах.
Уравнение Шредингера в том виде, в каком мы его записали, не учитывает каких-либо магнитных эффектов. Их, правда, можно приближенно принять во внимание, добавив в уравнение еще другие члены. Но, как мы убедились раньше, магнетизм — это эффект существенно релятивистский, так что правильное описание движения электрона в произвольном электромагнитном поле можно обсуждать только в рамках надлежащего релятивистского уравнения. Правильное релятивистское уравнение для движения электрона было открыто Дираком через год после того, как Шредингер придумал свое уравнение; оно имеет совершенно другой вид. Мы его не успеем здесь изучить.
Прежде чем перейти к рассмотрению некоторых следствий из уравнения Шредингера, хотелось бы продемонстрировать, как оно выглядит для системы многих частиц. Мы не будем им пользоваться, а просто хотим показать вам его, чтобы подчеркнуть, что волновая функция y не просто обычная волна в пространстве, а функция многих переменных. Если частиц много, уравнение превращается в
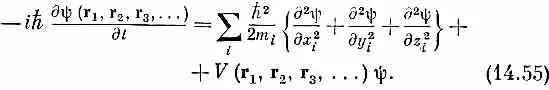
Потенциальная функция V — это то, что классически соответствует полной потенциальной энергии всех частиц. Если на частицы не действуют внешние силы, то функция V есть попросту электростатическая энергия взаимодействия всех частиц. Иначе говоря, если заряд i -й частицы равен Z i q e , то функция V просто равна
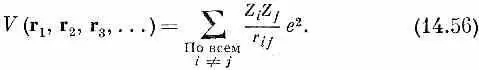
Читать дальше