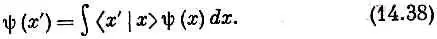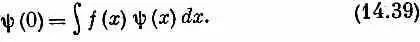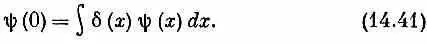Feynmann - Feynmann 9

Далее, амплитуда — это как раз то, что мы назвали функцией y ( х ) . Подобно атому а амплитуда < x '|y>, по­скольку она относится к тому же состоянию y, является той же функцией переменной х', а именно y ( х ' ) . Поэтому (14,37) можно переписать так;

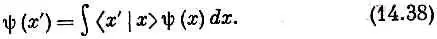
Уравнение должно выполняться для любого состояния y и, стало быть, для любой функции y ( х ) . Это требование обязано полностью определить природу амплитуды < x | х ' ), которая, конечно, есть попросту функция, зависящая от х и х ' .

Наша задача теперь состоит в том, чтобы отыскать функцию f ( х, х' ) , которая после умножения на y ( х ) и интегрирования по всем х даст как раз величину y ( х' ) . Но оказывается, что не существует математической функции, которая это умеет делать! По крайней мере не существует ничего похожего на то, что мы обычно имеем в виду под словом «функция».

Выберем какое-нибудь значение х', например 0, и опреде­лим амплитуду <0| x > как некую функцию х, скажем f ( х ) . Тогда (14.38) обратится в

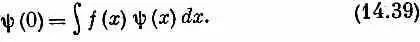
Какого же вида функция f ( х ) могла бы удовлетворить такому уравнению? Раз интеграл не должен зависеть от того, какие значения принимает y ( х ) при х, отличных от нуля, то ясно, что f ( х ) должна быть равна нулю для всех значений х, кроме нуля. Но если f ( х ) всюду равна нулю, то интеграл будет тоже равен нулю, и уравнение (14.39) не удастся удовлетворить. Возникает невозможная ситуация: нам нужно, чтобы функция была нулем всюду, кроме одной точки, и давала все же конечный интеграл. Что ж, раз мы не в состоянии сыскать функцию, которая так поступает, то простейший выход — просто сказать, что функция f (х) определяется уравнением (14.39). И именно f (х) — такая функция, которая делает (14.39) правильным. Функция, которая умеет это делать, впервые была изобретена Дираком и носит его имя. Мы обозначаем ее d ( х ) . Все, что о ней утверждается — это что функция d( х ) обладает странным свойством: если ее подставить вместо f ( х ) в (14.39), то интеграл выберет то значе­ние, которое y ( х ) принимает при х= 0 ; и поскольку интеграл не должен зависеть от y ( х ) при х, отличных от нуля, то функция d( х ) должна быть нулем всюду, кроме х= 0 . Словом, мы пишем

<0| x >=d( x ), (14.40)

где d ( х ) определяется соотношением

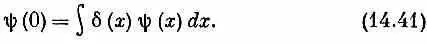
Посмотрите, что выйдет, если вместо y в (14.41) поставить частную функцию «1». Тогда получится

Иначе говоря, функция d( х ) обладает тем свойством, что всюду, кроме х= 0 , она равна нулю, но интеграл от нее конечен и равен единице. Приходится вообразить, что функция d( х ) обладает в одной точке такой фантастической бесконечностью, что полная площадь оказывается равной единице.

Как представить себе, на что похожа d-функция Дирака? Один из способов — вообразить последовательность прямо­угольников (или другую, какую хотите функцию с пиком), которая становится все уже и уже и все выше и выше, сохраняя все время единичную площадь, как показано на фиг. 14.2.

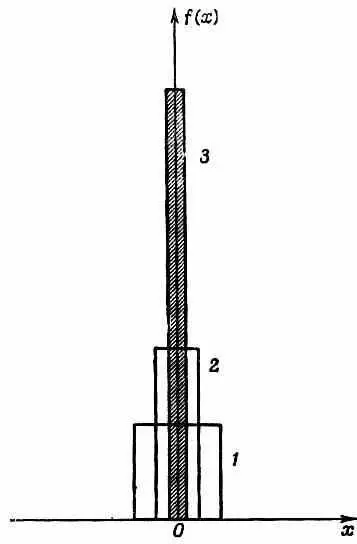
Фиг. 14.2. Последователь­ность функций, ограничиваю­щих единичную площадь, вид которых все сильнее и сильнее напоминает d -функцию.

Интеграл от этой функции от -Ґ до +Ґ всегда равен единице. Если вы умножите ее на произвольную функцию y( х ) и проин­тегрируете произведение, то получите нечто, приближенно сов­падающее со значением функции при х= 0 , причем приближение становится все лучше и лучше, по мере того как прямоугольники становятся уже и уже. Если хотите, можете представлять d-функцию посредством такого рода предельного процесса. Но единственно здесь важно то, что d-функция определена так, что (14.41) справедливо для каждой волновой функции y ( х ) .