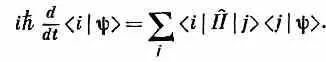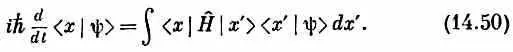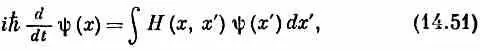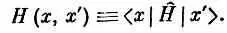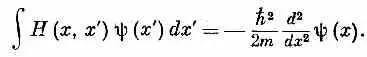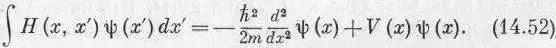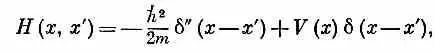Feynmann - Feynmann 9

и начнем.

В гл. 6 мы описали на языке гамильтониана Н ij ., как состоя­ния меняются во времени. Мы видели, что временная вариация различных амплитуд дается матричным уравнением

Это уравнение говорит, что изменение во времени каждой из амплитуд С i пропорционально сумме всех прочих амплитуд С j

с коэффициентами Н ij .

Как должно выглядеть (14.49) при континууме базисных состояний | x >? Вспомним сперва, что (14.49) можно также запи­сать в виде

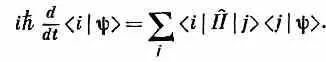
Теперь ясно, что делать. Для x -представления следует писать

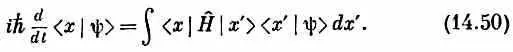
Сумма по базисным состояниям | j > заменяется интегралом по х'. Поскольку < х | Н ^ | х ' > должна быть какой-то функцией от x и х ', запишем ее как Н (х, х'), что соответствует Н if в (14.49). Тогда (14.50) это то же самое, что

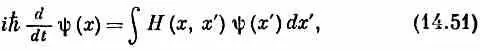
где

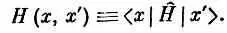
Согласно (14.51), быстрота изменения y в точке х зависела бы от значений y во всех других точках х '; множитель Н(х, х') — это амплитуда (в единицу времени) того, что электрон перепры­гнет из х' в x . Оказывается, однако, что в природе эта амплитуда всюду, кроме точек х ' , очень близких к х, равна нулю. Это озна­чает, как мы видели на примере цепочки атомов в начале главы [см. (14.12)], что правая часть (14.51) может быть полностью выражена только через y и ее производные по z в точке х.

Для частицы, которая свободно движется в пространстве, не подвергаясь действию каких-либо сил и возмущений, пра­вильный физический закон таков:

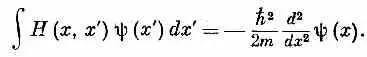
Откуда это получается? Это невозможно вывести из чего-либо нам уже известного. Это рождено в голове Шредингера, это вы­думано им в битве за понимание экспериментальных наблюдений реального мира. Может быть, какой-то ключ к тому, почему так должно быть, вам дадут размышления по поводу нашего вывода уравнения (14.12), которое проистекло из рассмотрения распро­странения электрона в кристалле.

Конечно, от свободных частиц проку мало. Что будет, если к частице приложить силы? Что ж, если действующая на частицу сила может быть описана с помощью скалярного потенциала V ( х ) (что означает, что речь идет не о магнитных силах, а об электрических) и если мы ограничимся низкими энергиями, чтобы иметь право пренебрегать теми сложностями, которые возникают при релятивистском движении, то гамильтониан, который укладывается в реальный мир, таков:

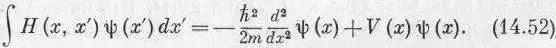
Опять-таки некоторый ключ к происхождению этого уравнения вы получите, если вернетесь к движению электрона в кристалле и посмотрите, как надо изменить уравнения, если энергия электрона медленно меняется от атома к атому, как если бы к кристаллу было приложено электрическое поле. Тогда член Е 0в (14.7) будет медленно меняться в зависимости от места и будет соответствовать новому слагаемому, появившемуся в (14.52). [Вас может удивить, отчего мы сразу перешли от (14.51) к (14.52), а не дали правильного выражения для амплитуды Н(х, х')= < х | Н ^ |х ' > . Да потому, что Н (х , х') можно написать только с помощью необычных алгебраических функций, а инте­грал в правой части (14.51) выражается через привычные вещи. Если вам это в самом деле интересно, то вот смотрите: Н (х, х') можно записать так:

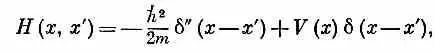
где d'' означает вторую производную 6-функции. Эту довольно странную функцию можно заменить чуть более удобным и пол­ностью ей равнозначным алгебраическим выражением