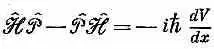
или

Опять классический результат. Справа стоит сила, так что мы вывели закон Ньютона! Но помните — это законы для операторов, которые дают средние величины. Они не описывают в деталях, что происходит внутри атома.
Существенное отличие квантовой механики в том, что р ^ х ^ не равно х ^ р ^ . Они отличаются на самую малость — на маленькое число h . Но все поразительные сложности интерференции волн и тому подобного проистекают из того небольшого факта, что х ^ р ^- р ^ х ^ не совсем нуль.
История этой идеи тоже интересна. С разницей в несколько месяцев в 1926 г. Гейзенберг и Шредингер независимо отыскали правильные законы, описывающие атомную механику. Шредингер изобрел свою волновую функцию y( х ) и нашел уравнение для нее, а Гейзенберг обнаружил, что природу можно было бы описывать и классическими уравнениями, лишь бы хр-рх было равно h / i , чего можно было добиться, определив их с помощью особого вида матриц. На нашем теперешнем языке он пользовался энергетическим представлением и его матрицами. И то и другое — и матричная алгебра Гейзенберга и дифференциальное уравнение Шредингера — объясняли атом водорода. Несколькими месяцами позднее Шредингер смог показать, что обе теории эквивалентны — мы только что это видели. Но две разные математические формы квантовой механики были открыты независимо.
* Во многих книжках для  используется один и тот же символ: физика в них одна и та же, да и удобнее все время обходиться без новых букв. А из контекста всегда ясно, что имеется в виду.
используется один и тот же символ: физика в них одна и та же, да и удобнее все время обходиться без новых букв. А из контекста всегда ясно, что имеется в виду.
* Уравнение (18.38) не означает , что | a >= x | y > [ср. (18.35)]. Сокращать на <���х| нельзя, потому что множитель х перед < x | y > для каждого состояния <���х| имеет свое значение. Это — значение координаты электрона в состоянии |х> [см. (18.40)].
* Можно выразить это и иначе. Какую бы функцию (т. е. состояние) вы ни выбрали, ее всегда можно представить в виде линейной комбинации базисных состояний, являющихся состояниями с определенной энергией. Поскольку в этой комбинации присутствует примесь состояний с более высокими энергиями, то средняя энергия окажется выше энергии основного состояния.
* Элемент объема мы обозначаем d Объем. Он попросту равен dxdydz , а интеграл берется от - Ґ до + Ґ по всем трем координатам.
Глав a 19
УРАВНЕНИЕ ШРЕДИНГЕРА
В КЛАССИЧЕСКОМ КОНТЕКСТЕ.
СЕМИНАР ПО СВЕРХПРОВОДИМОСТИ
§ 1. Уравнение Шредингера в магнитном поле
§ 2. Уравнение непрерывности для вероятностей
§ 3. Два рода импульсов
§ 4. Смысл волновой функции
§ 5. Сверхпроводимость
§ 6. Явление Мейсснера
& 7. Квантование потока
§ 8. Динамика сверхпроводимости
§ 9. Переходы Джозефсона
§ 1. Уравнение Шредингера в магнитном поле
Эту лекцию я читаю вам для развлечения. Захотелось посмотреть, что получится, если начать читать в немного ином стиле. В курс она не входит, и не думайте, что это попытка обучить вас в последний час чему-то новому. Я скорее воображаю, будто провожу семинар или будто делаю отчет об исследованиях перед более подготовленной аудиторией, перед людьми, которые в квантовой механике уже многое понимают. Основное различие между семинаром и регулярной лекцией в том, что на семинаре докладчик не приводит все стадии, всю алгебру выкладок. Он просто говорит: «Если вы проделаете то-то и то-то, то получится вот что», а в детали не входит. Вот и в этой лекции будут только высказываться идеи и приводиться результаты расчетов. А вы должны понимать, что вовсе не обязательно во всем немедленно и до конца разбираться, надо только верить, что если проделать все выкладки, то все так и получится.
Читать дальше

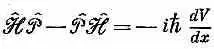

 используется один и тот же символ: физика в них одна и та же, да и удобнее все время обходиться без новых букв. А из контекста всегда ясно, что имеется в виду.
используется один и тот же символ: физика в них одна и та же, да и удобнее все время обходиться без новых букв. А из контекста всегда ясно, что имеется в виду.










