Feynmann - Feynmann 9

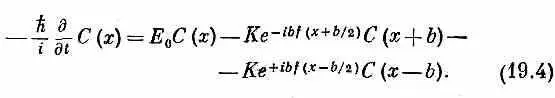
В нем три части. Во-первых, у электрона, который находится в точке х, есть некоторая энергия Е 0 . Это, как обычно, дает член Е 0 С ( х ) . Затем имеется член — КС(х + b ), т. е. амплитуда того, что электрон от атома n +1, расположенного в х + b , отпрыг­нул на шаг назад. Однако если это происходит в присутствии век­торного потенциала, то фаза амплитуды обязана сместиться со­гласно правилу (19.1). Если А х на расстоянии между соседними атомами заметно не изменяется, то интеграл можно записать по­просту в виде значения А х посредине, умноженного на расстоя­ние. Итак, произведение ( iq / h ) на интеграл равно ibf ( x + b /2) . А раз электрон прыгал назад, я этот сдвиг фазы отмечаю знаком минус. Это дает вторую часть. И точно так же имеется некоторая амплитуда того, что будет прыжок вперед, но на этот раз уже бе­рется векторный потенциал с другой стороны от х, на расстоя­нии b /2, и умножается на расстояние b . Это дает третью часть. В сумме получается уравнение для амплитуды того, что частица в поле, характеризуемом векторным потенциалом, окажется в точке х.

Но дальше мы знаем, что если функция С ( х ) достаточно плав­ная (мы берем длинноволновый предел) и если мы сдвинем ато­мы потеснее, то уравнение (14.4) (стр. 80) будет приблизитель­но описывать поведение электрона в пустоте. Поэтому следую­щим шагом явится разложение обеих сторон (19.4) по степеням b , считая b очень малым. К примеру, если b = 0 , то правая часть будет равна просто (Е 0 - 2 К)С(х), так что в нулевом приближе­нии энергия равняется Е 0 - 2 К. Затем пойдут степени b , но из-за того, что знаки показателей экспонент противоположны, оста­нутся только четные степени. В итоге, если вы разложите в ряд Тэйлора С(х), f ( x ) и экспоненты и соберете затем члены с b 2, вы получите

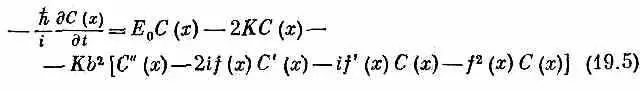
(штрихи обозначают дифференцирование по х).

Это ужасное нагромождение разных букв выглядит очень сложно. Но математически оно в точности совпадает с

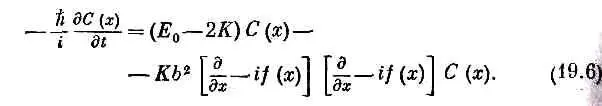
Вторая скобка, действуя на С ( х ) , даст С' ( х ) минус if ( x ) C ( x ) . Первая скобка, действуя на эти два члена, даст член с С", члены с первыми производными f ( x ) и с первой производной С ( х ) . А теперь вспомните, что решения в нулевом магнитном поле (см. гл. 11, §3) изображают частицу с эффективной массой m эфф, даваемой формулой

Kb 2 = h / m эфф

Если вы затем положите Е 0 =+ 2 К и снова вернетесь к f ( x ) = ( q / h ) A x , то легко убедитесь, что (19.6) это то же самое, что первая часть (19.3). (Происхождение члена с потенциальной энергией хорошо известно, и я не буду им заниматься.) Утверж­дение (19.1) о том, что векторный потенциал умножает все амп­литуды на экспоненциальный множитель, равнозначно правилу, что оператор импульса ( h / i )С заменяется на (h / i )С- q A, как мы и сделали в уравнении Шредингера (19.3).

§ 2. Уравнение непрерывности для вероятностей

Перехожу теперь ко второму пункту. Важную сторону урав­нения Шредингера отдельной частицы составляет идея о том, что вероятность обнаружить частицу в каком-то месте опреде­ляется квадратом абсолютной величины волновой функции. Для квантовой механики характерно также то, что вероятность сохраняется локально (т. е. в каждом отдельном месте). Когда вероятность обнаружить электрон в таком-то месте убывает, а вероятность обнаружить его в каком-то другом месте возрас­тает (так что полная вероятность не меняется), то что-то в про­межутке между этими местами должно было произойти. Иными словами, электрон обладает непрерывностью в том смысле, что если вероятность спадает в одном месте и возрастает в другом, то между этими местами должно что-то протекать. Так, если вы между ними поставите стенку, то это скажется на вероятностях и они станут не такими, как были. Следовательно, одно только сохранение вероятности не есть полная формулировка закона сохранения, все равно как одно только сохранение энергии не обладает такой глубиной и не представляет такой важности, как локальное сохранение энергии [см. гл. 27, § 1 (вып. 6)]. Если энергия исчезает, то этому должен соответствовать отток энергии от этого места. Вот и у вероятности хотелось бы обнару­жить такой же «ток». Хотелось бы, чтобы было так: если где-нибудь переменится плотность вероятности (вероятность об­наружить что-то там такое в единице объема), то чтобы можно было считать, что вероятность откуда-то сюда притекла (или утекла отсюда куда-то еще). Такой ток был бы вектором, кото­рый можно было бы толковать следующим образом: его x -ком понента была бы чистой вероятностью (в секунду и на единицу объема) того, что частица пройдет в направлении х через пло­скость, параллельную плоскости yz . Проход в направлении + x считается положительным потоком, а проход в обратную сто­рону — отрицательным потоком.