Feynmann - Feynmann 9

р-импульс=т v+ А . (19,15)

И вот оказывается, что в квантовой механике, вклю­чающей магнитные поля, с оператором градиента 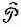свя­зан именно р -импульс, так что оператор скорости это (19.13).

Здесь я хотел бы немного отклониться от темы и по­яснить, почему так получается—отчего в квантовой механике должно быть нечто по­хожее на (19.15). Волновая функция меняется со временем, следуя уравнению Шредингера (19.3). Если бы я внезапно изменил векторный потенциал, то в первое мгновение вол­новая функция не изменилась бы, а изменилась бы только скорость ее изменения. Теперь представьте себе, что случится в следующих обстоятельствах. Пусть имеется длинный соленоид, в котором я создаю поток магнитного поля (поля В), как пока­зано на фиг. 19.2.

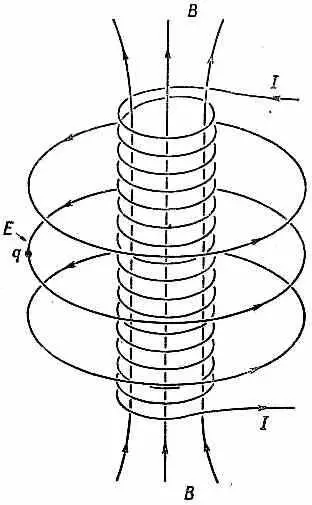
Фиг. 19.2 . Электрическое поле снаружи соленоида, ток в кото­ром увеличивается.

А поблизости сидит заряженная частица. До­пустим, что этот поток почти мгновенно с нуля вырастает до какого-то значения. Сперва векторный потенциал равен нулю, а потом я его включаю. Это означает, что я внезапно создаю кру­говой вектор-потенциал А. Вы помните, что криволинейный ин­теграл от А вдоль петли это то же самое, что поток поля В сквозь петлю [см. гл. 14, § 1 (вып. 5)]. И что же происходит, когда я мгновенно включаю векторный потенциал? Согласно квантовомеханическому уравнению, внезапное изменение А не вызывает внезапного изменения y; волновая функция пока та же самая. Значит, и градиент не изменился.

Но вспомните, что происходит электрически, когда я вне­запно включаю поток. В течение краткого времени, пока поток растет, возникает электрическое поле, контурный интеграл от которого равен скорости изменения потока во времени

Е=- д A / д t. (19.16)

Если поток резко меняется, то электрическое поле достигает огромной величины и оказывает сильное воздействие на частицу. Эта сила равна произведению заряда на электрическое поле; стало быть, в момент появления потока частица получает полный импульс (т. е. изменение в m v ), равный - q А. Иными словами, если вы подействуете на заряд векторным потенциалом, включив его внезапно, то этот заряд немедленно схватит mv -импульс, равный - q А. Но имеется нечто, не меняющееся не­медленно,— это разность между m v и - q А. Стало быть, сумма p = m v+ q A и есть то, что не меняется, если вы подвергаете вектор-потенциал внезапному изменению. Именно эту величину мы именуем p -импульсом, именно она играет важную роль в классической динамике; она же оказывается существенной и в квантовой механике. Эта величина зависит от характера волновой функции и является преемником оператора

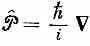
при наличии магнитного поля.

§ 4. Смысл волновой функции

Когда Шредингер впервые открыл свое уравнение, он открыл заодно, что закон сохранения (19.8) есть следствие этого урав­нения. Но он неправильно решил, что Р это плотность элект­рического заряда электрона, a J— плотность электрического тока, т. е. он думал, что электроны взаимодействуют с элект­ромагнитным полем через эти заряды и токи. Решая свои урав­нения для атома водорода и вычисляя y, он не вычислял ника­кой амплитуды (в то время еще не было амплитуд), а толковал это совершенно иначе. Атомное ядро было стационарно, вокруг же него текли токи; заряды Р и токи Jгенерировали электро­магнитные поля, и все вместе это излучало свет. Но вскоре, ре­шая задачу за задачей, он понял, что рассуждает не вполне правильно. И именно в этот момент Борн выдвинул весьма не­тривиальную идею. Именно Борн правильно (насколько нам известно) отождествил y в уравнении Шредингера с амплиту­дой вероятности, предположив, что квадрат амплитуды — это не плотность заряда, а всего лишь вероятность (на единицу объе­ма) обнаружить там электрон и что если вы находите элек­трон в некотором месте, то там окажется и весь его заряд. Вся эта идея принадлежит Борну.

Волновая функция y( r) электрона в атоме не описывает, стало быть, размазанного электрона с плавно меняющейся плотностью заряда. Электрон может быть либо здесь, либо там, либо где-то еще, но где бы он ни был, он всегда—точечный заряд. Но, с другой стороны, представим себе случай, когда огромное число частиц находится в одном и том же состоянии, очень боль­шое их число с одной и той же волновой функцией. Что тогда? Одна из них будет здесь, другая — там, и вероятность обнару­жить любую из них в данном месте пропорциональна yy*. Но поскольку частиц так много, то, если я посмотрю в какой-ни­будь объем dxdydz , я, вообще говоря, обнаружу там примерно yy * dxdydz частиц. Итак, когда y— волновая функция каж­дой из огромного количества частиц, поголовно пребывающих в одном и том же состоянии, то в этом случае yy* можно отождест­влять с плотностью частиц. Если в этих условиях все частицы несут одинаковые заряды q , то мы можем пойти дальше и отож­дествить y*y с плотностью электричества. Обычно, если yy* имеет размерность плотности вероятности, то yy* надо умножить на q , чтобы получить размерность плотности заряда. Для на­ших теперешних целей мы можем включить этот постоянный множитель в y и принять за плотность электрического заряда само yy*. Если помнить об этом, то J ^(тот ток вероятности, ко­торый я вычислил) можно будет считать просто плотностью электрического тока.