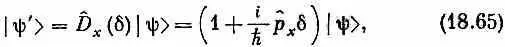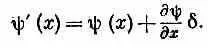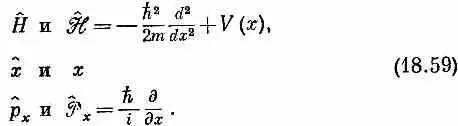
В этом перечне мы ввели новый символ 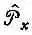 для алгебраического оператора ( h / i ) д / д x :
для алгебраического оператора ( h / i ) д / д x :

и поставили под  значок х, чтобы напомнить, что имеем пока дело с одной только x -компонентой импульса.
значок х, чтобы напомнить, что имеем пока дело с одной только x -компонентой импульса.
Результат этот легко обобщается на три измерения. Для других компонент импульса
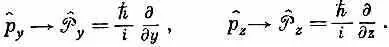
При желании можно даже говорить об операторе вектора импульса и писать
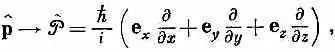
где е х , е y и е z — единичные векторы в трех направлениях. Можно записать это и еще изящнее:

Окончательный вывод наш таков: по крайней мере для некоторых квантовомеханических операторов существуют соответствующие им алгебраические операторы в координатном представлении. Все, что мы до сих пор вывели (с учетом трехмерности мира), подытожено в табл. 18.1. Каждый оператор может быть представлен в двух равноценных видах:
либо

либо

Теперь мы дадим несколько иллюстраций применения этих идей. Для начала выявим связь между 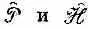 .
.
Если применить 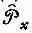 дважды, получим
дважды, получим
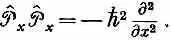
Это означает, что можно написать равенство
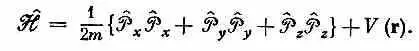
Или, в векторных обозначениях,
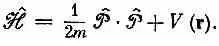
(Члены в алгебраическом операторе, над которыми нет символа оператора ^, означают простое умножение.) Это уравнение очень приятно, потому что его легко запомнить, если вы еще не забыли курса классической физики. Хорошо известно, что энергия (нерелятивистская) состоит из кинетической энергии р 2 /2 m плюс потенциальная, а у нас 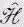 — тоже оператор полной энергии. Этот результат произвел на некоторых деятелей столь сильное впечатление, что они начали стремиться во что бы то ни стало вбить студенту в голову всю классическую физику, прежде чем приступить к квантовой. (Мы думаем иначе!) Параллели очень часто обманчивы. Если у вас есть операторы, то важен порядок различных множителей, а в классическом уравнении он безразличен.
— тоже оператор полной энергии. Этот результат произвел на некоторых деятелей столь сильное впечатление, что они начали стремиться во что бы то ни стало вбить студенту в голову всю классическую физику, прежде чем приступить к квантовой. (Мы думаем иначе!) Параллели очень часто обманчивы. Если у вас есть операторы, то важен порядок различных множителей, а в классическом уравнении он безразличен.
Таблица 18.1 · АЛГЕБРАИЧЕСКИЕ ОПЕРАТОРЫ В КООРДИНАТНОМ ПРЕДСТАВЛЕНИИ

В гл. 15 мы определили оператор р ^ х через оператор смещения D ^ x [см. формулу (15.27)]:
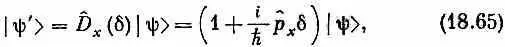
где d — малое смещение. Мы должны показать, что это эквивалентно нашему новому определению. В соответствии с тем, что мы только что доказали, это уравнение должно означать то же самое, что и
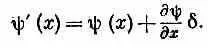
Но в правой части стоит просто разложение y ( x + d ) в ряд Тэйлора, а y ( x +d)— то, что получится, если сместить состояние влево на б (или сдвинуть на столько же вправо систему координат). Оба наши определения р ^ согласуются!
Читать дальше

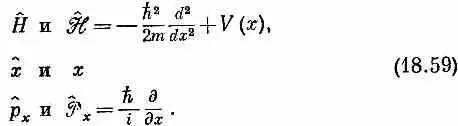
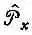 для алгебраического оператора ( h / i ) д / д x :
для алгебраического оператора ( h / i ) д / д x :
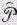 значок х, чтобы напомнить, что имеем пока дело с одной только x -компонентой импульса.
значок х, чтобы напомнить, что имеем пока дело с одной только x -компонентой импульса.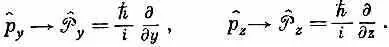
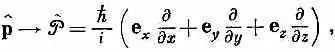



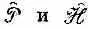 .
.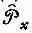 дважды, получим
дважды, получим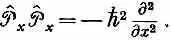
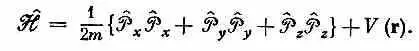
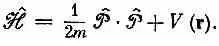
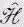 — тоже оператор полной энергии. Этот результат произвел на некоторых деятелей столь сильное впечатление, что они начали стремиться во что бы то ни стало вбить студенту в голову всю классическую физику, прежде чем приступить к квантовой. (Мы думаем иначе!) Параллели очень часто обманчивы. Если у вас есть операторы, то важен порядок различных множителей, а в классическом уравнении он безразличен.
— тоже оператор полной энергии. Этот результат произвел на некоторых деятелей столь сильное впечатление, что они начали стремиться во что бы то ни стало вбить студенту в голову всю классическую физику, прежде чем приступить к квантовой. (Мы думаем иначе!) Параллели очень часто обманчивы. Если у вас есть операторы, то важен порядок различных множителей, а в классическом уравнении он безразличен.