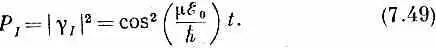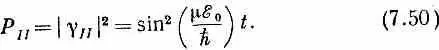Feynmann - Feynmann 8a

К примеру, предположим, что при t =0 наша молекулярная система была в верхнем энергетическом состоянии | I >, а это требует [из уравнения (7.40)], чтобы g I =1 и g II =0 при t =0. Для такого случая должно быть а =1 и b =0. Вероятность того, что молекула окажется в том же состоянии | I > в какой-то позднейший момент t , равна квадрату модуля g I , или

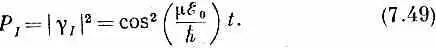
Точно так же и вероятность того, что молекула окажется в состоянии | II >, дается квадратом модуля g II :

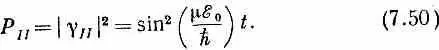
Пока x мало и пока мы находимся в резонансе, вероятности даются простыми колебательными функциями. Вероятность быть в состоянии | I > падает от единицы до нуля и возрастает опять, а вероятность быть в состоянии | II > растет от нуля до единицы и наоборот. Изменение обеих вероятностей во времени показано на фиг. 7.5.

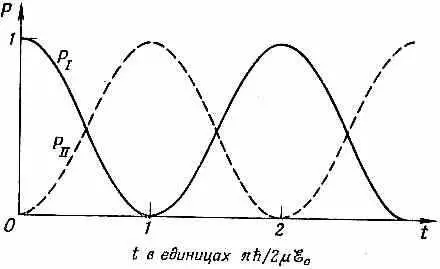
Фиг. 7.5. Вероятности обоих состояний моле­кулы аммиака в синусоидальном электрическом поле.

Нечего и говорить, что сумма обеих вероятностей всегда равна единице; ведь молекула всегда на­ходится в каком-то состоянии.

Положим, что прохождение через полость занимает у мо­лекулы время Т. Если сделать полость как раз такой длины, чтобы было mx 0 Т/ h = p /2, то молекула, ныряющая в нее в состоянии | I >, наверняка вынырнет из нее в состоянии | II >. Если она вошла в полость в верхнем состоянии, то выйдет из полости в нижнем. Иными словами, ее энергия упадет, и эта потеря энергии не сможет перейти ни во что другое, а только в механизм, который генерирует поле. Детали, которые по­могли бы вам разглядеть, как именно энергией молекулы питаются колебания полости, не так уж просты; однако нам и не нужно все эти детали изучать, потому что имеется принцип сохранения энергии. (Мы могли бы, если бы это было нужно, изучить их, но тогда нам пришлось бы иметь дело с квантовой механикой поля в полости наряду с квантовой механикой атома.)

Подытожим. Молекула входит в полость, поле полости, колеблющееся с как раз нужной частотой, индуцирует перехо­ды с верхнего состояния на нижнее, и высвобождаемой энергией питается осциллирующее поле. В работающий мазер молекулы доставляют достаточно энергии для того, чтобы поддержива­лись колебания полости, ее хватает не только на то, чтобы воз­местить потери в полости, но и на то, чтобы небольшие избытки энергии извлекались из полости. Итак, молекулярная энергия превращается в энергию внешнего электромагнитного поля.

Вспомним, что перед входом в полость нам приходилось пользоваться фильтром, который разделял пучок так, что в полость входило только верхнее состояние. Легко показать, что, если бы мы начали с молекул в нижнем состоянии, процесс пошел бы в другую сторону и энергия от полости отбиралась бы. Если пустить в полость нефильтрованный пучок, то сколько молекул будет отбирать энергию от полости, столько же из них будет отдавать ей свою энергию, и в итоге ничего не случится. В настоящем мазере, конечно, не обязательно делать ( m x 0T / h ) точно равным p/2. И при других значениях (кроме точных кратных p) существует какая-то вероятность переходов из состояния | I > в состояние | II >. Но при этих других значе­ниях прибор уже не имеет к. п. д., равного 100%; многие из молекул, покидающие полость, могли бы снабдить ее энергией, но не сделали этого.

На самом деле и скорости молекул неодинаковы; они рас­пределены по Максвеллу. Это означает, что идеальные периоды времени для разных молекул окажутся различными, и невоз­можно получить к. п. д., равный 100%, сразу для всех моле­кул. Вдобавок имеется еще одно усложнение, которое, правда, легко принять во внимание, но на этой стадии мы не будем им за­ниматься. Вы помните, что электрическое поле обычно меня­ется в полости от места к месту. Когда молекулы дрейфуют вдоль полости, электрическое поле близ молекул меняется как-то очень сложно, сложнее, чем предположенное нами обыч­ное синусоидальное колебание. Ясно, что для точного решения задачи следовало бы воспользоваться более сложными интег­рированиями, но общая идея остается прежней.