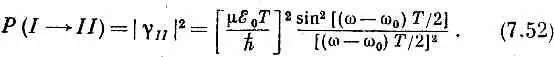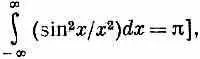Feynmann - Feynmann 8a

Можно мазеры устраивать и иначе. Не отделять прибором Штерна — Герлаха атомы в состоянии | I > от атомов в состоя­нии | II >, а собрать атомы в какой-то полости (в газообразном или твердом виде) и как-то переселить их из состояния | II > в состояние | I >. Один такой способ применяется в так назы­ваемом трехуровневом мазере. Для него используются атомные системы с тремя уровнями энергии (фиг. 7.6) и со следующими специальными свойствами.

Фиг. 7.6. Уровни энергии «трехуровневого» мазера.

Система поглощает излучение (ска­жем, свет) с энергией hw 1 и переходит от низшего уровня энер­гии Е II к какому-то более высокому уровню Е ' , а затем быстро испускает фотоны с энергией hw 2и переходит в состояние |/> с энергией Е I . У состояния | I > большое время жизни, так что его населенность может возрасти; создаются условия, благо­приятствующие работе мазера между состояниями | I > и | II >. Хотя такой прибор называют «трехуровневым» мазером, но сама мазерная процедура на самом деле происходит так же, как и у описанной нами двухуровневой системы.

Лазер — это всего-навсего мазер, действующий на свето­вых частотах. «Полость» лазера обычно состоит попросту из двух зеркал, между которыми генерируются стоячие волны.

§ 5 . Переходы вне резонанса

Наконец, хотелось бы выяснить, как изменяются состояния в условиях, когда частота полости, хотя и близка к w 0, но не совпадает с ней. Эту задачу можно было бы решить точно, но мы не будем пытаться это делать, а обратимся к важному слу­чаю малого электрического поля и малого промежутка време­ни Т, так что mx 0 T / h много меньше единицы. Тогда даже в слу­чае уже изученного нами идеального - резонанса вероятность перехода очень мала. Будем исходить опять из того, что g I =1 и g II =0. Тогда мы вправе ожидать, что в течение всего времени Т наша величина g I останется близкой к единице, а g II будет малой по сравнению с единицей, и задача облегчается. Из вто­рого уравнения (7.45) мы можем подсчитать g II , принимая g I равной единице и интегрируя от t =0 до t = T . Получается

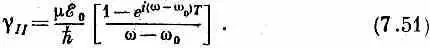
Это та величина g II , которая стоит в (7.40), и она дает амплитуду того, что переход из состояния | I > в состояние | II > произой­дет за время Т. Вероятность Р ( I ® II ) такого перехода равна

|g II | 2, или

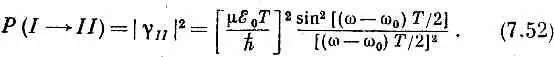
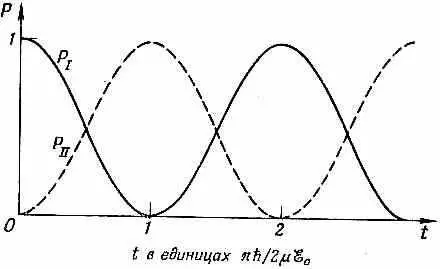
Интересно начертить эту вероятность при фиксированном времени T как функцию частоты полости, чтобы посмотреть, насколько чувствительна она к частотам близ резонансной ча­стоты w 0. Кривая Р ( I ® II ) показана на фиг. 7.7.

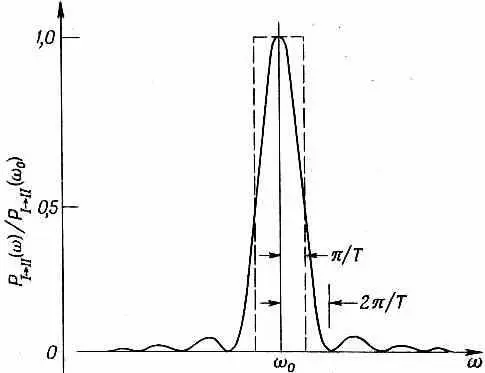
Фиг. 7.7. Вероятность перехода для молекулы аммиака как функция частоты.

(Вертикаль­ная шкала была подогнана так, чтобы в пике была единица, для этого разделили на величину вероятности при w=w 0.) С подобными кривыми мы встречались в теории дифракции, так что они должны быть вам знакомы. Кривая довольно резко падает до нуля при

(w-w 0)=2p/ T и никогда при больших отклонениях частоты снова не достигает заметной величины. Почти вся площадь под кривой лежит в пределах ±p/ T . Можно показать [с помощью формулы

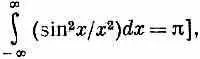
что площадь под кривой равна 2 p / T и совпадает с площадью выделен­ного штрихованной линией прямоугольника.

Посмотрим, что это дает для реального мазера. Возьмем разумное время пребывания молекулы аммиака в полости, ска­жем 1 мсек. Тогда для f 0=24000 Мгц можно подсчитать, что вероятность падает до нуля при отклонениях ( f - f 0 )/ f 0=1/ f 0 T , т. е. порядка 5·10 -8. Очевидно, что для заметных вероятностей перехода частоты должны очень точно совпадать с w 0. Этот эффект является основой той большой точности, которой можно достичь в «атомных» часах, работающих на принципе мазера.