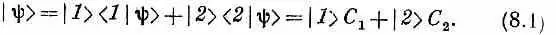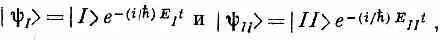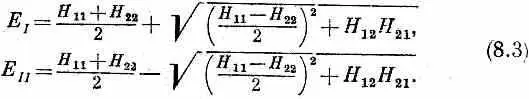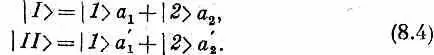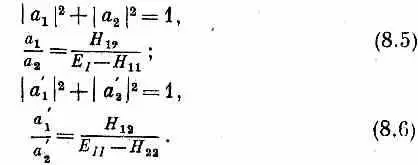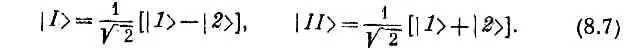Feynmann - Feynmann 8a

Для удобства подытожим важнейшие уравнения, выведенные в гл. 7, Пусть первоначально в качестве базисных состояний были приняты | 1 > и | 2 > . Тогда любое состояние |y> пред­ставляется их линейной комбинацией:

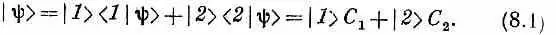
Амплитуды С i (под этим подразумеваются как C 1 так и С 2) удовлетворяют двум линейным дифференциальным уравнениям

где и i , и j принимают значения 1 и 2.

Когда члены гамильтониана H ij не зависят от t , то два состояния с определенной энергией (стационарные), которые мы обозначим

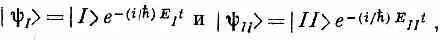
обладают энергиями

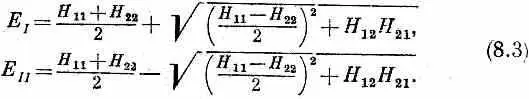
Для каждого из этих состояний оба С имеют одинаковую зависимость от времени. Векторы состояний | I > и | II >, кото­рые отвечают стационарным состояниям, связаны с нашими первоначальными базисными состояниями | 1 > и | 2 > формулами

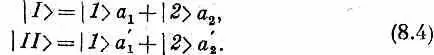
Здесь а —комплексные постоянные, удовлетворяющие равен­ствам

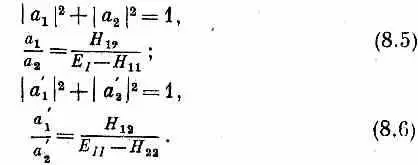
Если H 11и H 22между собой равны, скажем оба равны Е 0 , а H 12= H 21=- А, то E I = E 0+ A , Е II =Е 0 -А, и состоя­ния | I > и | II > особенно просты:

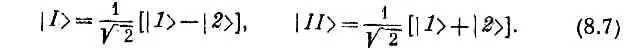
Эти результаты мы хотим теперь использовать, чтобы рас­смотреть ряд интересных примеров, взятых из химии и физики. Первый пример — это ион молекулы водорода. Положительно ионизированная молекула водорода состоит из двух протонов и одного электрона, как-то бегающего вокруг них. Каких состояний можно ожидать для этой системы, если расстояние между протонами велико? Ответ вполне ясен: электрон распо­ложится вплотную к одному протону и образует атом водорода в его наинизшем состоянии, а другой протон останется одиноч­кой, положительным ионом. Значит, когда два протона удале­ны друг от друга, то можно себе наглядно представить одно физическое состояние, в котором электрон «придан» одному из протонов. Существует, естественно, и другое, симметричное первому состояние, в котором электрон находится возле вто­рого протона, а ионом оказывается первый протон. Эту пару состояний мы и сделаем базисными, обозначив их | 1 > и | 2 >. Они показаны на фиг. 8.1.

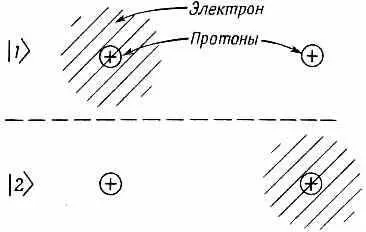
Фиг. 8.1. Совокупность базисных состояний для двух протонов и электрона.

Конечно, на самом деле у электрона возле протона имеется множество состояний, потому что их комбинация может существовать в виде одного из возбуждён­ных состояний атома водорода. Но нас сейчас не интересует это разнообразие состояний, мы будем рассматривать лишь случай, когда атом водорода пребывает в наинизшем состоя­нии — своем основном состоянии,— и пренебрежем на время спином электрона. Мы просто предположим, что для всех на­ших состояний спин электрона направлен вверх по оси z.

Чтобы убрать электрон из атома водорода, требуется 13,6 эв энергии. Столько же энергии — очень много по нашим тепе­решним масштабам — понадобится и на то, чтобы электрон ока­зался на полпути между протонами (коль скоро сами протоны сильно удалены друг от друга). Так что по классическим поня­тиям электрону немыслимо перескочить от одного протона к другому. Однако в квантовой механике это возможно, хоть и не очень вероятно. Существует некая малая амплитуда того, что электрон уйдет от одного протона к другому. Тогда в пер­вом приближении каждое из наших базисных состояний | 1 > и | 2 > будет иметь энергию Е 0 , равную просто сумме энергий атома водорода и протона. Матричные элементы Н 11 и H 22гамильтониана мы можем принять приближенно равными Е 0 . Другие матричные элементы Н 12 и Н 21 , представляющие собой амплитуды перехода электрона туда и обратно, мы опять за­пишем в виде - А.