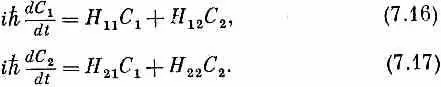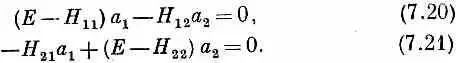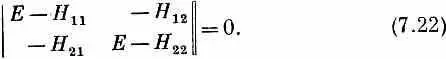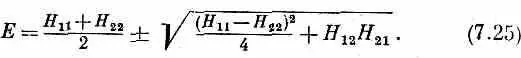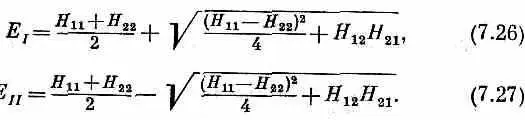Feynmann - Feynmann 8a

H 12= H 21=- А. (7.15)

Теперь с этими новыми значениями Н ij надо решать гамильтоновы уравнения (6.43). Мы могли бы их решить просто, как делали это прежде, но поскольку нам не раз, видимо, представится случай решать системы с двумя состояниями, то давайте уж решим их раз и навсегда в общем случае произвольного Н ij , считая только, что со временем оно не меняется.

Мы ищем общее решение пары гамильтоновых уравнений

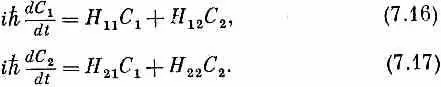
Это линейные дифференциальные уравнения с постоянными коэффициентами. Значит, всегда можно найти решения, яв­ляющиеся экспоненциальными функциями независимой пере­менной t . Сперва отыщем решения, в которых С 1 и С 2одина­ково зависят от времени; возьмем пробные функции

Поскольку это решение отвечает состоянию с энергией E = h w ,

то можно прямо написать

где Е пока неизвестна и должна быть определена так, чтобы дифференциальные уравнения (7.16) и (7.17) выполнялись. При подстановке С 1 и С 2из (7.18) и (7.19) в дифференци­альные уравнения (7.16) и (7.17) производные дают просто - iE / h , умноженное на С 1 или C 2, так что слева остается попросту ЕС 1 или ЕС 2 . Сокращая общие экспоненциальные множители, получаем

или после перестановки членов

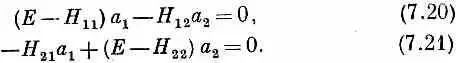
У такой системы однородных алгебраических уравнений не­нулевые решения для а 1и а 2будут лишь тогда, когда опре­делитель, составленный из коэффициентов при а 1 и а 2, равен нулю, т. е. если

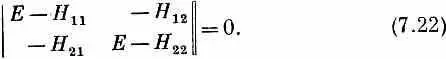
Но когда уравнений два и неизвестных тоже два, то можно обойтись и без столь возвышенных представлений. Каждое из уравнений (7.20) и (7.21) дает отношение двух коэффициентов a 1и а 2, и эти два отношения должны быть равны. Из (7.20) мы имеем

а из (7.21)

Приравнивая эти отношения, получаем, что Е должно удовле­творять равенству

( E - H 11 )( E - H 22 )- H 12 H 21 = 0 .

То же получилось бы и из (7.22). В любом случае для Е получается квадратное уравнение с двумя решениями:

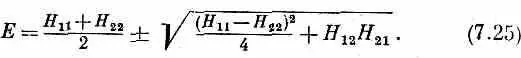
Энергия E может иметь два значения. Заметьте, что оба они вещественны, потому что Н 11 и H 22вещественны, а Н 12 Н 21 , равное Н 12 H 12=| H 12| 2, тоже вещественно, да к тому же положительно.

Пользуясь тем же соглашением, что и раньше, обозначим большую энергию E I , а меньшую Е II . Имеем

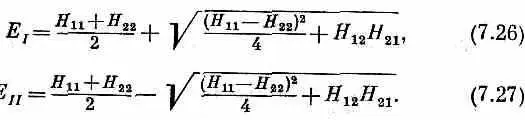
Подставив каждую из этих энергий по отдельности в (7.18) и (7.19), получим амплитуды для двух стационарных состояний (состояний определенной энергии). Если нет каких-либо внеш­них возмущений, то система, первоначально бывшая в одном из этих состояний, останется в нем навсегда, у нее только фаза будет меняться.

Наши результаты можно проверить на двух частных слу­чаях. Если H 12= H 21=0, то получается E I = H 11и E II = H 22. А это бесспорно правильно, потому что тогда уравнения (7.16) и (7.17) не связаны и каждое представляет состояние с энер­гией H 11и H 22. Далее, положив H 11= H 22= E 0и H 21= H 12=- А, придем к найденному выше решению: