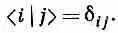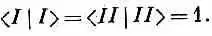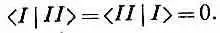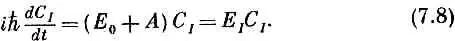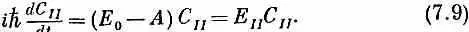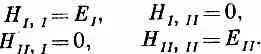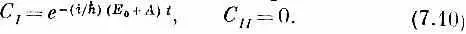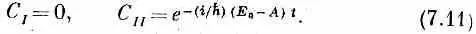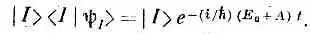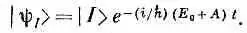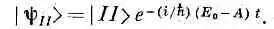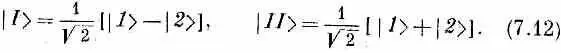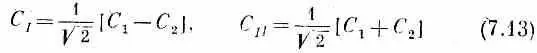Feynmann - Feynmann 8a

Зачем все это нужно? С какой целью все это делается? Дело в том, что состояния |I> и |II> могут быть приняты за новую совокупность базисных состояний, особенно подхо­дящую для описания стационарных состояний молекулы ам­миака. Вы помните, что требования к совокупности базисных состояний были таковы:

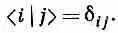
Мы уже сами сделали так, чтобы было

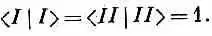
Из (7.5) и (7.7) легко вывести, что и

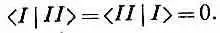
Амплитуды С I =< I |Ф> и С II =< II |Ф> того, что любое состояние |Ф> окажется в одном из наших новых базисных со­стояний | I > и | II >, обязаны также удовлетворять гамильтонову уравнению вида (6.39). И действительно, если мы просто вычтем друг из друга два уравнения (7.2) и (7.3) и продиф­ференцируем по t , то убедимся, что

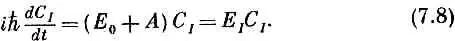
А взяв сумму (7.2) и (7.3), увидим

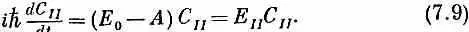
Если за базисные состояния взять | I > и | II >, то гамильтонова матрица очень проста:

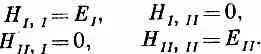
Заметьте, что каждое из уравнений (7.8) и (7.9) выглядит очень похоже на то, что получалось в гл. 6, § 6, для уравнения си­стемы с одним состоянием. Они дают простую экспоненциальную зависимость от времени, отвечающую определенной энергии.

С ростом времени амплитуды пребывания в каждом из состоя­ний ведут себя независимо.

Найденные нами раньше стационарные состояния |y I> и |y II> тоже являются, конечно, решениями уравнений (7.8) и (7.9). У состояния |y I> (для которого С 1 =-С 2 )

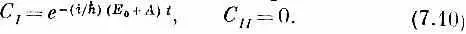
А у состояния |y II> (для которого С 1= С 2)

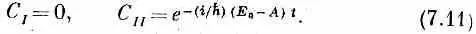
Пусть мы теперь умножили (7.10) на вектор состояния |/>; тогда получится

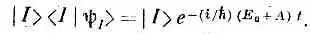
Вспомним, однако, что |I>

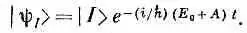
Иначе говоря, вектор состояния стационарного состояния |y I> не отличается от вектора состояния базисного состояния | I > ничем, кроме экспоненциального множителя, связанного с энергией состояния. И действительно, при t=0

|y I>=| I >;

физическая конфигурация у состояния )/> та же самая, что и у стационарного состояния с энергией Е 0 + А. Точно так же для второго стационарного состояния получается

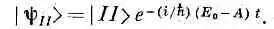
Состояние | II >— это просто стационарное состояние с энер­гией Е 0 - А при t = 0 . Стало быть, оба наших новых базисных состояния | I > и | II > физически имеют вид состояний с опреде­ленной энергией, но с изъятым экспоненциальным временным множителем, так что они могут быть приняты за базисные со­стояния, не зависящие от времени. (В дальнейшем нам будет удобно не отличать стационарные состояния |y I> и |y II> от их базисных состояний | I > и | II >, ведь различаются они только очевидными временными множителями.)

Подведем итог. Векторы состояний | I > и | II > — это пара базисных векторов, приспособленных для описания состояний молекулы аммиака с определенной энергией. Они связаны с нашими исходными базисными векторами формулами

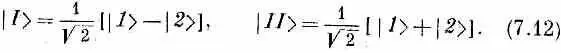
Амплитуды пребывания в | I > и | II > связаны с С 1 и С 2 форму­лами

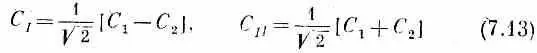
Всякое состояние может быть представлено линейной комби­нацией | 1 > и |2 > (с коэффициентами С 1 и С 2) или линейной ком­бинацией базисных состояний с определенной энергией | I > и | II > (с коэффициентами С I и С II ) . Итак,