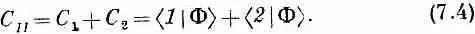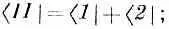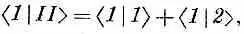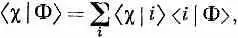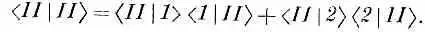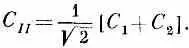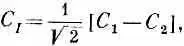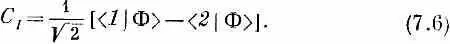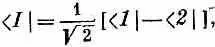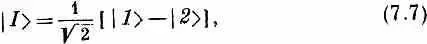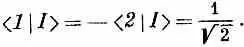Feynmann - Feynmann 8a

Если бы азот не мог перескакивать вверх или вниз, нам пришлось бы принять А равным нулю, и оба энергетических уровня (с энергией Е 0) налезли бы один на другой. Истинные уровни не таковы; их среднее значение Е 0 , но они разведены на ±А, т. е. промежуток между энергиями двух состояний равен 2А. Поскольку А на самом деле мало, то и разница в энергиях очень мала.

Чтобы возбудить электрон внутри атома, требуются до­вольно высокие энергии, нужны фотоны оптического или уль­трафиолетового диапазона. Чтобы возбудить вибрации молекул, требуются инфракрасные фотоны. Если речь идет о возбужде­нии вращений, различия в энергиях состояний соответствуют фотонам в далекой инфракрасной области. Но разность энер­гий 2А меньше их всех, меньше инфракрасных энергий, она приходится на микроволновой диапазон. Опытным путем было найдено, что существует пара уровней энергии с промежутком 10 -4 эв, что отвечает частоте 24000 Мгц. Это, очевидно, озна­чает, что 2 A = hf , где f =24000 Мгц (отвечает волне длиной 1 1/ 4 см). Значит, перед нами молекула с переходами, которые вызывают испускание микроволн, а не свет в обычном смысле.

Для дальнейшей работы нам понадобится немного более удобное описание этих двух состояний с определенной энер­гией. Представим, что мы построили амплитуду С 11 из суммы двух чисел C 1 и С 2:

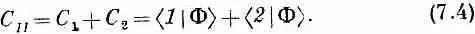
Что бы это могло означать? Очень просто: это амплитуда того, что состояние |Ф> окажется в новом состоянии |//>, в котором амплитуды первоначальных базисных состояний равны между собой, Иначе говоря, когда мы пишем С II = < II |Ф>, то мы впра­ве абстрагироваться в уравнении (7.4) от |Ф>, поскольку оно вы­полняется при любых Ф, и писать

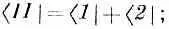
это означает то же самое, что и

Амплитуда того, что состояние (II} окажется в состоянии |1>, равна

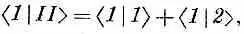
а это, конечно, равняется просто единице, поскольку и |1>, и |2> суть базисные состояния. И амплитуда обнаружения состояния |II> в состоянии \2у тоже равна единице, так что у состояния |II> одинаковы амплитуды оказаться в каждом из базисных состояний |1> и |2> .

Но тут всплывает новая трудность. У состояния | II > пол­ная вероятность оказаться то ли в одном базисном состоянии, то ли в другом получается больше единицы. Но это всего лишь означает, что вектор состояния неудачно «отнормирован». Чтобы исправить дело, надо вспомнить, что всегда для любого состояния обязано быть < II | II >=1. Использовав общее соотношение

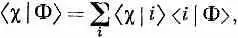
полагая, что и Ф, и c суть состояние II , и суммируя по ба­зисным состояниям |1> и |2> , получаем

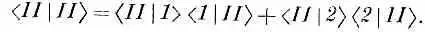
Это даст, как положено, единицу, если мы изменим наше оп­ределение С II [см. уравнение (7.4)] и примем

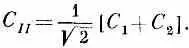
Таким же путем можно построить и амплитуду

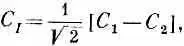
или

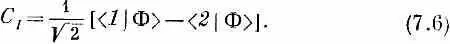
Эта амплитуда есть проекция состояния |Ф> на новое состоя­ние | I >, обладающее амплитудами противоположного знака, для пребывания в состояниях |1> и |2> . А именно (7.6) означает то же самое, что и

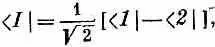
или

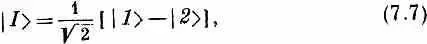
откуда следует