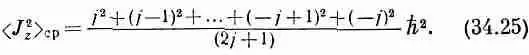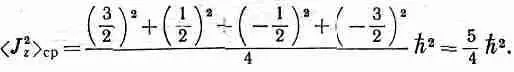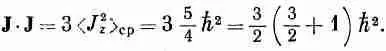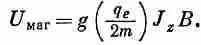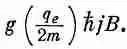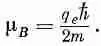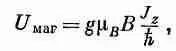Feynmann - Feynmann 7

J · J = J 2 x + J 2 y + J 2 z

Поскольку это скаляр, то он должен оставаться одним и тем же для любой ориентации спина. Предположим, что мы случай­но выбрали образец какой-либо атомной системы и произвели измерения либо величины J 2 x , либо J 2 y, либо J 2 z — среднее

значение любой из них должно быть тем же самым. (Ни одно из направлений не имеет особого преимущества перед любым другим.) Следовательно, среднее значение J· J равно просто утроенной средней величине любой компоненты, скажем J 2 z :

< J· J > cp =3< J 2 z >.

Но поскольку J· J при любой ориентации одно и то же, его среднее, разумеется, будет постоянной величиной

J· J= 32 z> cp. (34.24)

Если же мы теперь скажем, что то же самое уравнение будет использоваться и в квантовой механике, то можем легко найти 2 z> ср. Нам просто нужно взять сумму (2j+1) возможных значений J 2 z и поделить ее на число всех значений:

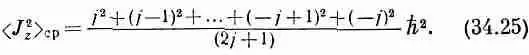
Вот что получается для системы со спином 3/ 2:

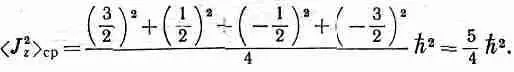
Отсюда мы заключаем, что

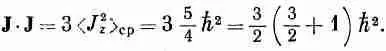
На вашу долю остается доказать, что соотношение (34.25) вместе с (34.24) дает в результате

Хотя в рамках классической физики мы бы думали, что наи­большее возможное значение z-компоненты Jравно просто абсолютной величине J, именно Ц( J· J), в квантовой механике максимальное значение J z всегда немного меньше его, ибо jh всегда меньше Ц[j(j+1)]h. Момент количества движения ни­когда не направлен «полностью вдоль оси z».

§ 8. Магнитная энергия атомов

Теперь я снова хочу поговорить о магнитном моменте. Я уже говорил, что в квантовой механике магнитный момент атомной системы может быть связан с моментом количества движения соотношением (34.6):

где - q e — заряд, а m — масса электрона.

Атомные магнитики, будучи помещены во внешнее магнит­ное поле, приобретут дополнительную магнитную энергию, которая зависит от компоненты их магнитного момента в на­правлении поля. Мы знаем, что

U маг =- m · В.(34.28) Выбирая ось z вдоль направления поля В, получаем

U маг = m z В. (34.29) А используя уравнение (34.27), находим

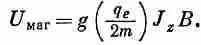
Согласно квантовой механике, величина J z может принимать только такие значения: jh, (j-1)h,...,- jh. Поэтому магнитная энергия атомной системы не произвольна, допустимы только некоторые ее значения. Например, максимальная величина энергии равна

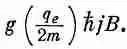
Величину q e h /2 m обычно называют «магнетоном Бора» и обоз­начают через m B :

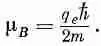
Возможные значения магнитной энергии будут следующими:

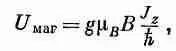
где J z / h принимает одно из следующих значений: j, (j-1), (j-2), ..., (-j+1), -j.

Другими словами, энергия атомной системы, помещенной в магнитное поле, изменяется на величину, пропорциональную полю и компоненте J г . Мы говорим, что энергия атомной маг­нитной системы «расщепляется магнитным полем на 2j+1 уровня». Например, атомы со спином j = 3 / 2 , энергия которых вне магнитного поля равна U 0, в магнитном поле будут иметь четыре возможных значения энергии. Эти энергии можно изобра­зить на диаграмме энергетических уровней наподобие фиг. 34.5.