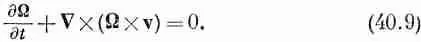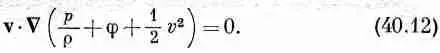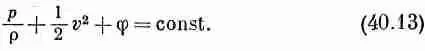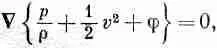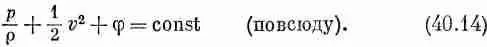Если нас интересует только поле скоростей, то из наших уравнений можно исключить давление. Взяв ротор обеих частей уравнения (40.8) и вспомнив, что r — величина постоянная, а ротор любого градиента равен нулю, а также использовав уравнение (40.3), находим
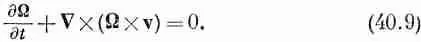
Это уравнение вместе с уравнениями
W=СXv (40.10)
и
С·v=0 (40.11)
полностью описывают поле скоростей v. На языке математики — если в некоторый момент мы знаем W ,то мы знаем ротор вектора скорости и, кроме того, знаем, что его дивергенция равна нулю, так что в этих физических условиях у нас есть все необходимое для определения скорости v повсюду. (Все это в точности напоминает нам знакомые условия в магнетизме, где С· B=0 и СX B= j/e 0c 2.) Таким образом, данная величина W определяет v точно так же, как jопределяет В. Затем из известного значения v уравнение (40.9) даст нам скорость изменения W, откуда мы можем получить новую W в следующий момент. Используя снова уравнение (40.10), найдем новое значение v и т. д. Теперь вы видите, как в эти уравнения входит весь механизм, необходимый для вычисления потока. Заметьте, однако, что эта процедура дает только скорости, а всю информацию о давлении мы потеряли.
Отметим особое следствие нашего уравнения. Если в какой-то момент времени t повсеместно W=0, то д W / д t тоже исчезает, так что W всюду останется равной нулю и в момент t +Dt. Отсюда следует, что поток все время остается безвихревым. Если вначале поток не вращался, то он так никогда и не начнет вращаться. При этом уравнения, которые мы должны решать, таковы:
С·v=0, СXv=0.
Они в точности напоминают уравнения электростатики или магнитостатики в пустом пространстве. Позднее мы вернемся к ним и рассмотрим некоторые частные задачи.
§ 3. Стационарный поток; теорема Бернулли
Вернемся к уравнениям движения (40.8), но ограничимся теперь приближением «стационарного» потока. Под стационарным потоком я подразумеваю поток, скорость которого в любом месте жидкости никогда не изменяется. Жидкость в любой точке постоянно заменяется новой жидкостью, движущейся в точности таким же образом. Картина скоростей всегда выглядит одинаково, т. е. v представляет статическое векторное поле. Как в магнитостатике мы рисовали силовые линии, так и здесь можно начертить линии, которые всегда касательны к скорости жидкости (фиг. 40.5).
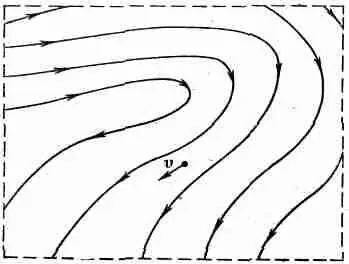
Фиг. 40.5. Линии тока стационарного потока.
Эти линии называются «линиями тока». Для стационарного потока они действительно представляют реальные пути частиц жидкости. (В нестационарном потоке картина линий тока меняется со временем, однако в любой момент времени она не представляет пути частиц жидкости.)
Стационарность потока вовсе не означает, что ничего не происходит — частички жидкости движутся и изменяют свои скорости. Это означает только то, что д v / д t =0. Если теперь мы скалярно умножим уравнение движения на v, то слагаемое v·(WXv) выпадет и у нас останется только
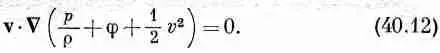
Согласно этому уравнению, при малых перемещениях в направлении скорости жидкости величина внутри скобок не изменяется. В стационарном потоке все перемещения направлены вдоль линий тока; поэтому уравнение (40.12) говорит, что для всех точек вдоль линии тока
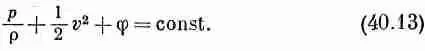
Это и есть теорема Бернулли. Постоянная, вообще говоря, для различных линий тока может быть разной; мы знаем только, что левая часть уравнения (40.13) постоянна всюду вдоль данной линии тока. Заметьте, кстати, что если стационарный поток безвихревой, т. е. если для него W=0, то уравнение движения (40.8) дает нам соотношение
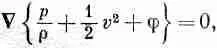
так что
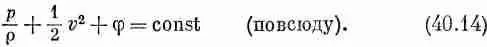
Читать дальше