Feynmann - Feynmann 7

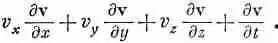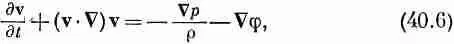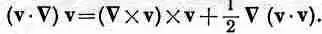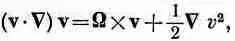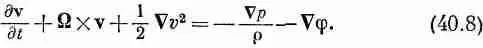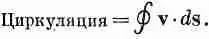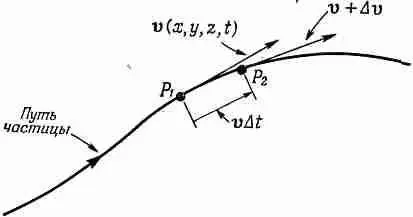
Фиг. 40.4. Ускорение частицы жидкости.

Фактически в направлении оси х она пере­двинется на расстояние v x D t , в направлении оси у — на рас­стояние v у D t , а в направлении оси z — на расстояние v z D t . Мы видим, что если v (х, у, z , t ) — скорость частицы в момент t , то скорость той же самой частицы в момент t + D t представ­ляет величину v (х + D x, у + D y , z+ D z, t + D t ), причем

D x = v x D t , D y = v y D t и D z = v z D t .

Из определения частных производных [вспомните уравнения гл. 2, вып. 5] мы с точностью до членов первого порядка получаем

Ускорение же D v / D t будет равно

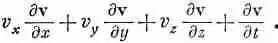
Считая С вектором, это можно записать символически:

Обратите внимание, что, даже когда д v / д t =0, т. е. когда скорость в данной точке не изменяется, ускорение все же останется. Примером может служить вода, текущая с постоян­ной скоростью по кругу: она ускоряется даже тогда, когда ско­рость в данной точке не изменяется. Причина, разумеется, состоит в том, что скорость данной капельки воды, которая первоначально находилась в одной точке, моментом позднее будет иметь другое направление — это центростремительное ускорение.

Остальная часть нашей теории — чисто математическая: нахождение решения уравнения движения, полученного под­становкой ускорения (40.5) в (40.4), т. е.

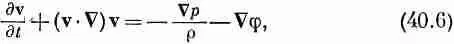
где слагаемое с вязкостью уже выброшено. Воспользовав­шись известным тождеством из векторного анализа, это уравнение можно переписать по-другому:

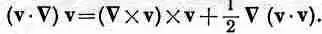
Если определить новое векторное поле W как ротор скорости v, т. е.

то векторное тождество можно записать так:

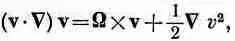
а наше уравнение движения (40.6) примет вид

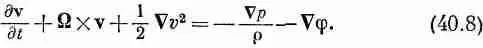
Вы можете проверить эквивалентность уравнений (40.6) и (40.8), расписывая их по компонентам и сравнивая их, восполь­зовавшись при этом выражением (40.7).

Если W всюду равно нулю, то такой поток мы называем безвихревым (или потенциальным). В гл. 3, § 5 (вып. 5), мы уже определяли величину, называемую циркуляцией векторного поля. Циркуляция по любой замкнутой петле в жидкости равна криволинейному интегралу от скорости жидкости в дан­ный момент времени вокруг этой петли:

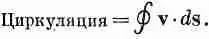
Циркуляция на единицу площади для бесконечно малой петли по теореме Стокса будет тогда равна СX v. Таким образом, Wпредставляет собой циркуляцию вокруг единичной площади (перпендикулярной направлению W). Кроме того, ясно, что если в любое место жидкости поместить маленькую соринку (именно соринку, а не бесконечно малую точку), то она будет вращаться с угловой скоростью W/2. Попытайтесь доказать это. Вы можете также попробовать доказать, что для ведра воды на вращающемся столике Wравна удвоенной локальной угловой скорости воды.