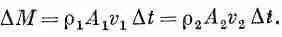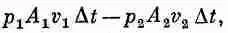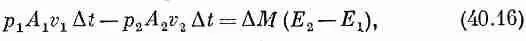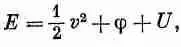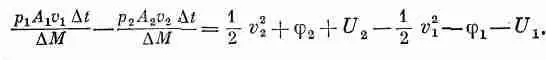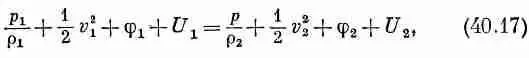Feynmann - Feynmann 7

Оно в точности напоминает уравнение (40.13), за исключением того, что теперь постоянная во всей жидкости одна и та же. На самом деле теорема Бернулли не означает ничего боль­шего, чем утверждение о сохранении энергии. Подоб­ные теоремы о сохранении дают нам массу информации о потоке без детального решения уравнений. Теорема Бернулли на­столько важна и настолько проста, что мне бы хотелось пока­зать вам, как можно ее получить другим способом, отличным от тех формальных вычислений, которые мы только что про­вели. Представьте себе пучок линий тока, образующих трубку тока (фиг. 40.6, а).

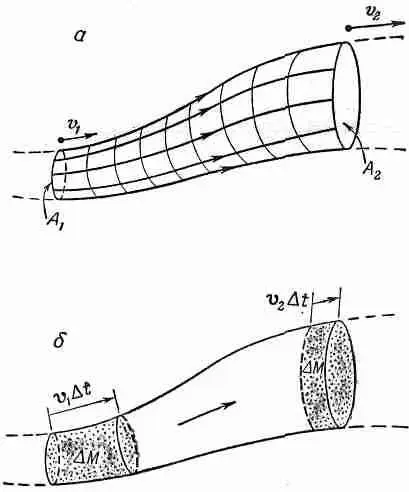
Фиг. 40.6. Движение жидкости в трубке.

Поскольку стенки трубки образуются ли­ниями тока, то жидкость через них не протекает. Обо­значим площадь на одном конце трубки через A 1, скорость жидкости через v 1 , плотность через r 1а потенциальную энер­гию через j 1. Соответствующие величины на другом конце трубки мы обозначим через A 2 , v 2 , r 2и j 2. После короткого интервала времени Dt жидкость на одном конце передвинется на расстояние v 1 D t , а жидкость на другом конце — на расстоя­ние v 2Dt (см. фиг. 40.6, б). Сохранение массы требует, чтобы масса, которая вошла через A 1 была равна массе, которая

вышла через А 2 . Изменение масс в этих двух концах должно быть одинаково:

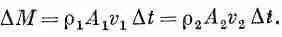
Таким образом, мы получаем равенство

Оно говорит нам, что при постоянном r скорость изменяется обратно пропорционально площади трубки тока.

Вычислим теперь работу, произведенную давлением в жидкости. Работа, произведенная над жидкостью, входящей со стороны сечения А 1 , равна р 1A 1v 1АDt, а работа, произведен­ная в сечении А 2 , равна p 2 A 2 v 2 D t . Следовательно, полная работа, произведенная над жидкостью, заключенной между A 1и А 2 , будет

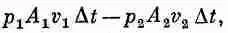
что должно быть равно возрастанию энергии массы жидкости DM при прохождении от А 1 до А 2 . Другими словами,

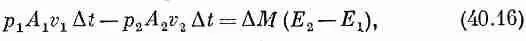
где Е 1 — энергия единицы массы жидкости в сечении А 1 , а Е 2 — энергия единицы массы в сечении А 2 . Энергию единицы массы жидкости можно записать в виде

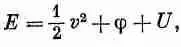
где 1/ 2 v 2 — кинетическая энергия единицы массы, j — потен­циальная энергия, a U — дополнительный член, представляю­щий внутреннюю энергию единицы массы жидкости. Внутрен­няя энергия может соответствовать, например, тепловой энер­гии сжимаемой жидкости или химической энергии. Все эти величины могут изменяться от точки к точке. Воспользо­вавшись выражением для энергии в уравнении (40.16), получим

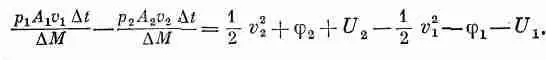
Но мы видели, что DМ=rDvDt, и получили

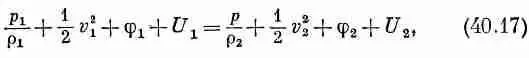
а это как раз приводит нас к результату Бернулли, где имеется дополнительный член, представляющий внутреннюю энергию. Если жидкость несжимаемая, то внутренняя энергия с обеих сторон одна и та же и мы снова убеждаемся в справедливости уравнения (40.14) вдоль любой линии тока.

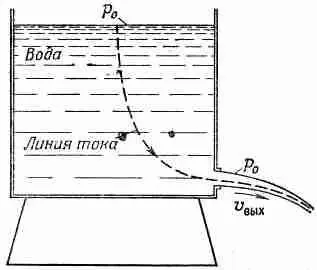
Рассмотрим теперь неко­торые простые примеры, в которых интеграл Бернулли позволяет нам сразу описать поток. Предположим, что из отверстия вблизи дна резервуара вы­текает вода (фиг. 40.7).