Feynmann - Feynmann 6

С новым членом, добавленным Максвеллом в уравнение IV, мы смогли записать полевые уравнения в терминах А и j в форме, которая проста и сразу же позволяет выявить существование электромагнитных волн. Для многих практических целей еще будет удобно использовать первоначальные урав­нения в терминах Е и В. Но они — по ту сторону горы, на ко­торую мы уже вскарабкались. Теперь мы можем посмотреть вокруг. Все будет выглядеть иначе, — нас ожидают новые, прекрасные пейзажи.

*Это не совсем так. Поля могут быть «поглощены», если попадут в область, в которой есть заряды.

Это значит, что где-то могут быть созданы другие поля, которые наложатся на эти поля и «погасят»их в результате деструктивной интерференции (см. гл. 31, вып. 3)

* К-2— вторая по высоте вершина мира в северо-западных отрогах Гималаев, называемых Каракорум.—- Прим. р е д .

*Выбор значения С · А называется «выбором калибровки». Изменение А за счет добавления С y называется «калибровочным преобра­зованием». Выбор (18.23) называют «калибровкой Лоренца».

I ' лав a 19

ПРИНЦИП НАИМЕНЬШЕГО ДЕЙСТВИЯ

Добавление, сделанное после лекции

Когда я учился в школе, наш учитель фи­зики, по фамилии Бадер, однажды зазвал меня к себе после урока и сказал: «У тебя вид такой, как будто тебе все страшно надоело; послу­шай-ка об одной интересной вещи». И он рас­сказал мне нечто, что мне показалось поистине захватывающим. Даже сейчас, хотя с тех пор прошла уже уйма времени, это продолжает меня увлекать. И всякий раз, когда я вспоми­наю о сказанном, я вновь принимаюсь за ра­боту. И на этот раз, готовясь к лекции, я поймал себя на том, что вновь анализирую все то же самое. И, вместо того чтобы гото­виться к лекции, я взялся за решение новой задачи. Предмет, о котором я говорю,— это принцип наименьшего действия.

Вот что сказал мне тогда мой учитель Бадер: «Пусть, к примеру, у тебя имеется частица в поле тяжести; эта частица, выйдя откуда-то, свободно движется куда-то в другую точку. Ты подбросил ее, скажем, кверху, а она взлетела, а потом упала.

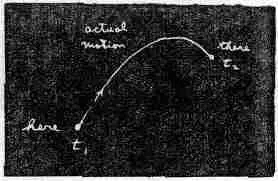
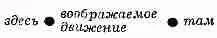
От исходного места к конеч­ному она прошла за какое-то время. Попробуй теперь какое-то другое движение. Пусть для того, чтобы перейти «отсюда сюда», она двигалась уже не так, как рань­ше, а вот так:

но все равно очутилась на нужном месте в тот же самый момент вре­мени, что и раньше».

«И вот,— продолжал учитель,— если ты подсчитаешь кине­тическую энергию в каждый момент времени на пути частицы, вычтешь из нее потенциальную энергию и проинтегрируешь разность по всему тому времени, когда происходило движение, то увидишь, что число, которое получится, будет больше, чем при истинном движении частицы.

Иными словами, законы Ньютона можно сформулировать не в виде F=ma, а вот как: средняя кинетическая энергия минус средняя потенциальная энергия достигает своего самого наи­меньшего значения на той траектории, по которой предмет двигается в действительности от одного места к другому.

Попробую пояснить тебе это чуть понятнее.

Если взять поле тяготения и обозначить траекторию час­тицы x ( t ), где х — высота над землей (обойдемся пока одним измерением; пусть траектория пролегает только вверх и вниз, а не в стороны), то кинетическая энергия будет 1/ z m ( dx / dt ) 2 , а потенциальная энергия в произвольный момент времени будет равна mgx .

Теперь я для какого-то момента движения по траектории беру разность кинетической и потенциальной энергий и интегри­рую по всему времени от начала до конца. Пусть в начальный момент времени t t движение началось на какой-то высоте, а кончилосъ в момент t 2на дру­гой определенной высоте.