Feynmann - Feynmann 6

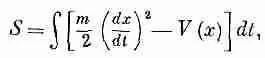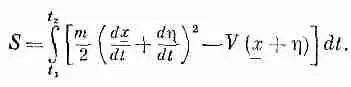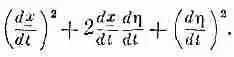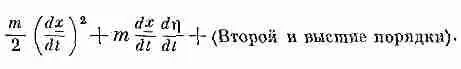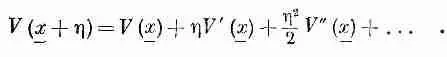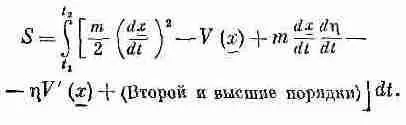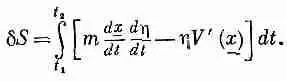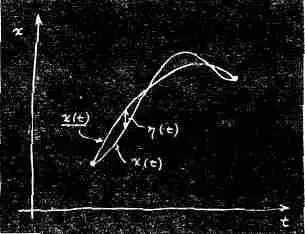
Идея состоит в том, что если мы подсчитаем действие S на пути x ( t ), то разность между этим S и тем дейст­вием, которое мы вычислили для пути x ( t ) (для простоты

оно будет обозначено S), или разность между S и S, должна быть в первом приближении по h нулем. Они могут отли­чаться во втором порядке, но в первом разность обязана быть нулем.

И это должно соблюдаться для любой h. Впрочем, не со­всем для любой. Метод требует принимать во внимание только те пути, которые все начинаются и кончаются в одной и той же паре точек, т. е. всякий путь должен начинаться в определен­ной точке в момент t 1и кончаться в другой определенной точке в момент t 2 . Эти точки и моменты фиксируются. Так что наша функция h(отклонение) должна быть равна нулю на обоих концах: h(t 1)=0 и h(t 2)=0. При этом условии наша математическая задача становится полностью опре­деленной.

Если бы вы не знали дифференциального исчисления, вы могли бы проделать такую же вещь для отыскания минимума обычной функции f ( x ). Вы бы задумались над тем, что случится, если взять f ( x ) и прибавить к х малую величину h , и доказы­вали бы, что поправка к f ( x ) в первом порядке по h долж­на в минимуме быть равна нулю. Вы бы подставили x + h вместо х и разложили бы f ( x + h ) с точностью до первой сте­пени h . . ., словом, повторили бы все то, что мы намерены

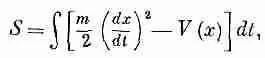
Итак, идея наша заключается в том, что мы подставляем x ( t ) = x ( t ) + - h ( t ) в формулу для действия

где через V ( x ) обозначена потенциальная энергия. Производная dx / dt — это, естественно, производная от x ( t ) плюс производ­ная от h ( t ), так что для действия я получаю такое выражение:

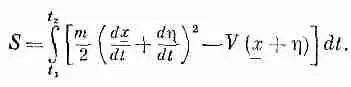
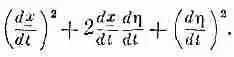
Теперь это нужно расписать подетальней. Для квадратич­ного слагаемого я получу

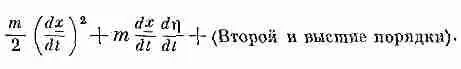
Но постойте-ка! Ведь мне не нужно заботиться о порядках выше первого. Я могу убрать все слагаемые, в которых есть h 2и высшие степени, и ссыпать их в ящик под названием «второй и высшие порядки». Из этого выражения туда попадет только одна вторая степень, но из чего-то другого могут войти и выс­шие. Итак, часть, связанная с кинетической энергией, такова:

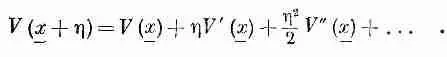
Дальше нам нужен потенциал V в точках x+h. Я считаю т) малой и могу разложить V ( x ) в ряд Тэйлора. Приближенно это будет V ( x ); в следующем приближении (из-за того, что здесь стоят обычные производные) поправка равна h , умноженной на скорость изменения V по отношению к x; и т. д.:

Для экономии места я обозначил через V производную F по х. Слагаемое с h 2и все, стоящие за ним, попадают в категорию «второй и высшие порядки». И о них больше нечего беспо­коиться. Объединим все, что осталось:

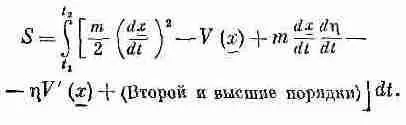
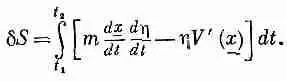
Если мы теперь внимательно взглянем на это, то увидим, что два первых написанных здесь члена отвечают тому действию S , которое я написал бы для искомого истинного пути х . Я хочу сосредоточить ваше внимание на изменении S , т. е. на разности между S и тем S , которое получилось бы для истинного пути. Эту разность мы будем записывать как d S и назовем ее вариа­цией S . Отбрасывая «второй и высшие порядки», получаем для dS

Теперь задача выглядит так. Вот передо мной некоторый интеграл. Я не знаю еще, каково это х , но я твердо знаю, что, какую h я ни возьму, этот интеграл должен быть равен нулю. «Ну что ж,— подумаете вы,— единственная возможность для этого — это чтобы множитель при h был равен нулю». Но как быть с первым слагаемым, где есть d h / dt ? Вы скажете: «Если h обращается в ничто, то и ее производная такое же ничто; зна­чит, коэффициент при d h / dt должен тоже быть нулем». Ну это не совсем верно. Это не совсем верно потому, что между откло­нением h и его производной имеется связь; они не полностью независимы, потому что h (t) должно быть нулем и при t t и при t 2 .