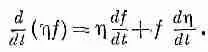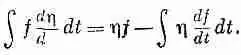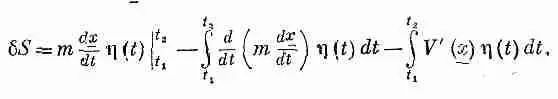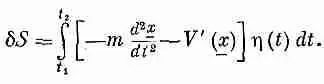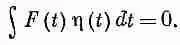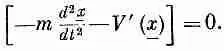При решении всех задач вариационного исчисления всегда пользуются одним и тем же общим принципом. Вы чуть сдвигаете то, что хотите варьировать (подобно тому, как это сделали мы, добавляя h), бросаете взгляд на члены первого порядка, затем расставляете все так, чтобы получился интеграл в таком виде: «сдвиг (h), умноженный на что получится», но чтобы в нем не было никаких производных от h (никаких d h / dt ). Непременно нужно так все преобразовать, чтобы осталось «нечто», умноженное на h . Сейчас вы поймете, отчего это так важно. (Существуют формулы, которые подскажут вам, как в некоторых случаях можно это проделать без каких-либо выкладок; но они не так уж общи, чтобы стоило заучивать их; лучше всего проделывать выкладки так, как это делаем мы.)
Как же я могу переделать член d h / dt , чтобы в нем появилось h? Я могу добиться этого, интегрируя по частям. Оказывается, что в вариационном исчислении весь фокус в том и состоит, чтобы расписать вариацию S и затем проинтегрировать по частям так, чтобы производные от h исчезли. Во всех задачах, в которых появляются производные, проделывается такой же фокус.
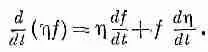
Припомните общий принцип интегрирования по частям. Если у вас есть произвольная функция f, умноженная на d h / dt и проинтегрированная по t , то вы расписываете производную от h f :
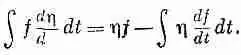
В интересующем вас интеграле стоит как раз последнее слагаемое, так что
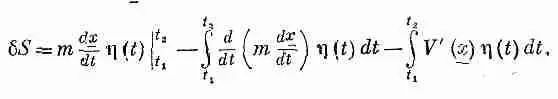
В нашей формуле для dS за функцию f принимается произведение т на dx / dt ; поэтому я получаю для d S выражение
В первый член должны быть подставлены пределы интегрирования t 1 и t 2. Тогда я получу под интегралом член от интегрирования по частям и последний член, оставшийся при преобразовании неизменным.
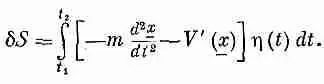
А теперь происходит то, что бывает всегда,— проинтегрированная часть исчезает. (А если не исчезает, то нужно переформулировать принцип, добавив условия, обеспечивающие такое исчезновение!) Мы уже говорили, что hна концах пути должна быть равна нулю. Ведь в чем состоит наш принцип? В том, что действие минимально при условии, что варьируемая кривая начинается и кончается в избранных точках. Это значит, что h(t 1)=0 и h(t 2)=0. Поэтому проинтегрированный член получается равным нулю. Мы собираем воедино остальные члены и пишем
Вариация S теперь приобрела такой вид, какой мы хотели ей придать: что-то стоит в скобках (обозначим его F ), и все это умножено на h(t) и проинтегрировано от t 1 до t 2 .
У нас вышло, что интеграл от какого-то выражения, умноженного на h(t), всегда равен нулю:
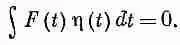
Стоит какая-то функция от t ; умножаю ее на h(t) и интегрирую ее от начала до конца. И какова бы ни была h, я получаю нуль. Это означает, что функция F(t) равна нулю. В общем-то это очевидно, но я на всякий случай покажу вам один из способов доказательства.
Пусть в качестве h ( t ) я выберу нечто, что равно нулю всюду, при всех t , кроме одного, заранее выбранного значения t . Оно
остается нулем, пока я не
дойду до этого t ,
затем оно подскакивает на мгновение и сразу же осаживает назад. Если вы берете интеграл от этой h , умноженной на какую-то функцию F , то единственное место, в котором вы получите что-то ненулевое,— это там, где h ( t ) подскакивало; и у вас получится значение F в этом месте на интеграл по скачку. Сам по себе интеграл по скачку не равен нулю, но после умножения на F он должен дать нуль. Значит, функция в том месте, где был скачок, должна оказаться нулем. Но ведь скачок можно было сделать в любом месте; значит, F должна быть нулем всюду.
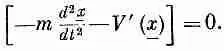
Читать дальше