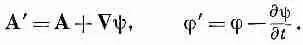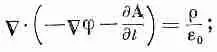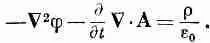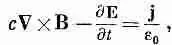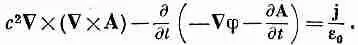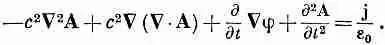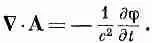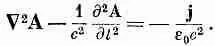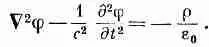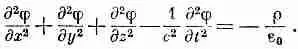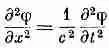Feynmann - Feynmann 6

(18.19)

Мы уже решили два из уравнений Максвелла и нашли, что для описания электромагнитных полей Е и В нужны четыре потенциальные функции: скалярный потенциал j и векторный потенциал А, который, разумеется, представляет три функции.

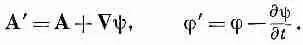
Итак, А определяет часть Е, так же как и В. Что же про­изойдет, когда мы заменим А на A'=A+Сy? В общем, Е долж­но было бы измениться, если не принять особых мер. Мы можем, однако, допустить, что А изменяется так, чтобы не влиять на поля Е и В (т. е. не меняя физики), если будем всегда изменять А и j вместе по правилам

(18.20)

Тогда ни В, ни Е, полученные из уравнения (18.19), не меня­ются.

Раньше мы выбирали С·А=0, чтобы как-то упростить уравнения статики. Теперь мы не собираемся так поступать; мы хотим сделать другой выбор. Но подождите немного, прежде чем мы скажем, какой это выбор, потому что позднее станет ясно, почему вообще делается выбор.

Сейчас мы вернемся к двум оставшимся уравнениям Максвел­ла, которые свяжут потенциалы и источники r и j. Раз мы можем определить А и j из токов и зарядов, то можно всегда получить Е и В из уравнений (18.16) и (18.19) и мы будем иметь другую форму уравнений Максвелла.

Начнем с подстановки уравнения (18.19) в С·E=r/e 0; получаем

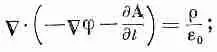
это можно записать еще в виде

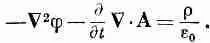
(18.21)

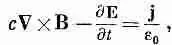
Таково первое уравнение, связывающее j и А с источниками, Наше последнее уравнение будет самым трудным. Мы начнем с того, что перепишем четвертое уравнение Максвелла:

а затем выразим В и Е через потенциалы, используя уравнения (18.16) и (18.19):

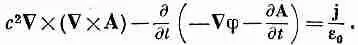
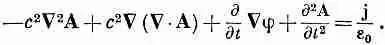
Первыйчлен можно переписать, используя алгебраическое тождество Vx (СXA) = С (С·A)-С 2A; мы получаем

(18.22)

Не очень-то оно простое!

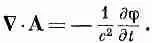
К счастью, теперь мы можем использовать нашу свободу в произвольном выборе дивергенции А. Сейчас мы собираемся сделать такой выбор, чтобы уравнения для А и для j разделились, но имели одну и ту же форму. Мы можем сделать это, выбирая

(18.23)

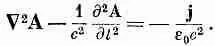
Когда мы поступаем так, то второе и третье слагаемые в уравнении (18.22) погашаются, и оно становится много проще:

(18.24)

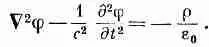
И. наше уравнение (18.21) для j принимает такую же форму:

(18.25)

Какие красивые уравнения! Они великолепны прежде всего потому, что хорошо разделились — с плотностью заряда стоит j, а с током стоит А. Далее, хотя левая сторона выглядит не­много нелепо — лапласиан вместе с ( d / dt ) 2 , когда мы раскроем ее, то обнаружим

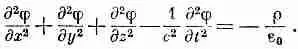
(18.26)

Это уравнение имеет приятную симметрию по х, у, z , t ; здесь (-1/с 2) нужно, конечно, потому, что время и координаты раз­личаются; у них разные единицы.

Уравнения Максвелла привели нас к нового типа уравнению для потенциалов j и А, но с одной и той же математической формой для всех четырех функций j, А х , А у и А г . Раз мы научились решать эти уравнения, то можем получить В и Е изСXЕ и-Сj- dA / dt . Мы приходим к другой форме электро­магнитных законов, в точности эквивалентной уравнениям Максвелла; с ними во многих случаях обращаться гораздо проще.

Фактически мы уже решали уравнение, весьма похожее на (18.26). Когда мы изучали звук в гл. 47 (вып. 4), мы имели уравнение в форме

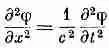
и видели, что оно описывает распространение волн в x-направлении со скоростью с. Уравнение (18.26) это соответствующее волновое уравнение для трех измерений. Поэтому в области, где больше нет зарядов и токов, решение этих уравнений не означает, что j и А — нули. (Хотя на самом деле нулевое решение есть одно из возможных решений.) Имеются решения, представляющие некоторую совокупность j и А, которые ме­няются со временем, но всегда движутся со скоростью с. Поля передвигаются вперед через свободное пространство, как в нашем примере в начале главы.