Feynmann - Feynmann 6

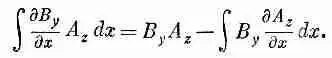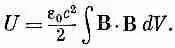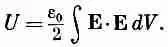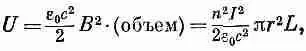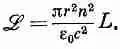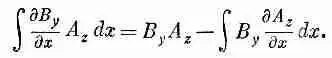
Теперь предположим, что наша система (имея в виду источники и поля) — конечная, так что, когда мы уходим на большие рас­стояния, все поля стремятся к нулю. Тогда при интегрировании по всему пространству подстановка B y A z на пределах интеграла дает нуль. У нас остается только В (дА г /дх); это, очевидно, есть часть от B y ( СX A ) y и, значит, от В·(СXA). Если вы вы­пишите остальные пять множителей, то увидите, что (17.47) на самом деле эквивалентно (17.46).

А теперь мы можем заменить (СXA) на В и получить

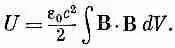
(17.48)

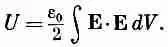
Мы выразили энергию в магнитостатическом случае только через магнитное поле. Выражение тесно связано с формулой, которую мы нашли для электростатической энергии:

(17.49)

Эти две энергетические формулы выделены потому, что иногда ими удобнее пользоваться. Обычно есть и более важная причина: оказывается, что для динамических полей (когда Е и В меняются со временем) оба выражения (17.48) и (17.49) остаются справедливыми, тогда как другие данные нами фор­мулы для электрической и магнитной энергий перестают быть верными — они годятся лишь для статических полей.

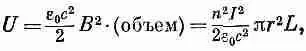
Если нам известно магнитное поле В одной катушки, мы можем найти коэффициент самоиндукции, приравнивая выра­жение для энергии (17.48) и 1/ 2жI 2. Посмотрим, что получится в результате для индуктивности длинного соленоида. Раньше мы видели, что магнитное поле в соленоиде однородно и В снаружи равно нулю. Величина поля внутри равна В=nI/e 0с 2 , где n — число витков на единицу длины намотки, а I — ток. Если радиус катушки r , а длина ее L (мы считаем, что L очень велика, чтобы можно было пренебречь краевыми эффектами, т. е. L > >r), то внутренний объем равен pr 2L. Следовательно, магнитная энергия равна

что равно 1/ 2 ^ I 2 . Или

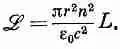
(17.50)

* Кстати, это не единственный способ установления соответствия между механическими и электрическими величинами.

* Мы пренебрегаем всеми тепловыми потерями энергии в сопротив­лении катушки. Эти потери требуют дополнительных затрат энергии источника, но не меняют энергии, которая тратится на индуктивность.

Глав а 18

УРАВНЕНИЯ МАКСВЕЛЛА

§ 1. Уравнения Максвелла

§ 2. Что дает добавка

§ 3. Все о класси­ческой физике

§ 4. Передвигаю­щееся поле

§ 5. Скорость света

§ 6. Решение уравнений Максвелла; потенциалы и волновое уравнение

§ 1. Уравнения Максвелла

В этой главе мы вернемся к полной системе из четырех уравнений Максвелла, которые мы приняли как отправной пункт в гл. 1 (вып. 5). , До сих пор мы изучали уравнения Максвелла не­большими частями, кусочками; теперь пора уже прибавить последнюю часть и соединить их все воедино. Тогда мы будем иметь полное и точное описание электромагнитных полей, которые могут изменяться со временем произвольным образом. Все сказанное в этой главе, если даже оно и будет противоречить чему-то сказанному ранее, правильно, а то, что говорилось ранее в этих случаях, неверно, потому что все высказанное ранее применялось к таким част­ным случаям, как, скажем, случаи постоянного тока или фиксированных зарядов. Хотя всякий раз, когда мы записывали уравнение, мы весьма старательно указывали ограничения, легко по­забыть все эти оговорки и слишком хорошо заучить ошибочные уравнения. Теперь мы можем изложить всю истину, без всяких ограни­чений (или почти без них).

Все уравнения Максвелла записаны в табл. 18.1 как словесно, так и в математических символах. Тот факт, что слова эквивалентны уравнениям, должен быть сейчас вам уже зна­ком — вы должны уметь переводить одну форму в другую и обратно.

Первое уравнение — дивергенция Е равна плотности заряда, деленной на e о,— правильно всегда. Закон Гаусса справедлив всегда как в динамических, так и в статических полях. Поток Е через любую замкнутую поверхность пропорционален заключенному внутри заряду. Третье уравнение — соответствующий общий закон для магнитных полей.