Feynmann - Feynmann 6

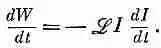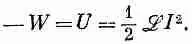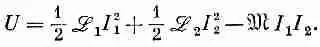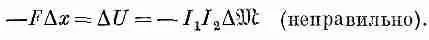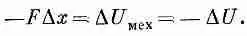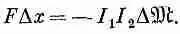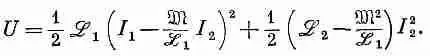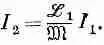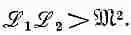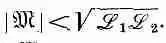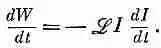
Подставляя вместо e ее выражение через токи из (17.34), имеем

(17.38)

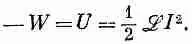
Интегрируя это уравнение, находим, что энергия, которая требуется от внешнего источника, чтобы преодолеть э. д. с. самоиндукции и создать ток (что должно равняться накоп­ленной энергии U), равна

(17.37)

Поэтому энергия, накопленная в индуктивности, равна 1/ 2ж I 2. Применяя те же рассуждения к паре катушек, изображен­ных на фиг. 17.8 или 17.9, мы можем показать, что полная электрическая энергия системы дается выражением

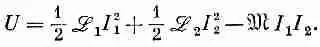
(17.38)

В самом деле, начиная с тока I=0 в обеих катушках, можно вна­чале включить ток I 1в катушке 1, оставляя I 2=0. Совершен­ная работа как раз равна l / 2 ж 1 l 1 2 . Но теперь, включая I 2, мы совершаем не только работу 1/ 2ж 2I 2 2против э. д. с. в цепи 2, но еще и добавочное количество работы —m I 1I 2, которая есть интеграл

от э. д. с. m ( dI z / dt ) в цепи 1, умноженный на теперь уже постоянный ток I 1в этой цепи.

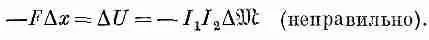
Пусть теперь нам нужно найти силу между любыми двумя катушками, по которым идут токи I 1и I 2. Прежде всего мы мог­ли бы использовать принцип виртуальной работы, взяв вари­ацию от энергии (17.38). Мы должны помнить, конечно, что при изменении относительного положения катушек единственной меняющейся величиной является коэффициент взаимной индук­ции m. Тогда мы могли бы записать уравнение виртуальной работы в виде

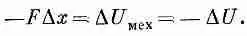
Это уравнение ошибочно, потому что, как мы видели раньше, в него включено только изменение энергии двух катушек и не включена энергия источников, которые поддерживают постоян­ными значения токов I 1 и I 2. Мы понимаем теперь, что эти источники должны поставлять энергию для компенсации инду­цированных э. д. с. в катушках во время их движения. Если мы хотим правильно применить принцип виртуальной работы, то должны включить и эти энергии. Но мы видели, что можно сделать и короче — использовать принцип виртуальной рабо­ты, помня, что полная энергия — это взятая с обратным знаком энергия U мех(то что мы называем «механической энергией»). Поэтому силу можно записать в виде

(17.39)

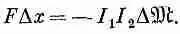
Тогда сила между катушками дается выражением

Воспользуемся выражением (17.38) для энергии системы из двух катушек, чтобы показать, какое интересное неравенство существует между взаимной индукцией m и коэффициен­тами самоиндукции ж 1и ж 2 двух катушек. Ясно, что энергия двух катушек должна быть положительной. Если мы начинаем с нулевых токов в обеих катушках и увеличиваем эти токи до некоторых значений, то тем самым мы увеличиваем энергию всей системы. В противном случае токи самопроизвольно воз­растут и будут отдавать энергию остальному миру — вещь невероятная! Далее, наше выражение для энергии (17.38) можно с

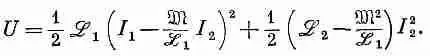
таким же успехом записать в следующей форме:

(17.40)

Это просто алгебраическое преобразование. Эта величина долж­на быть всегда положительна при любых значениях I 1и I 2. В частности, она должна быть положительна, когда I 2вдруг примет особое значение:

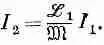
(17.41)

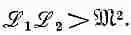
Но при таком значении I 2первое слагаемое в (17.40) равно ну­лю. Если энергия положительна, то последнее слагаемое в (17.40) должно быть больше нуля. Мы получаем требование, что

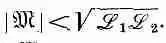
Таким образом, мы доказали общее соотношение, что величина взаимной индукции m любых двух катушек обязательно меньше или равна геометрическому среднему двух коэффициен­тов самоиндукции (сам m может быть положителен или отри­цателен в зависимости от выбора знаков для токов I tи I 2):