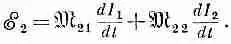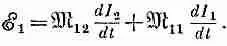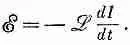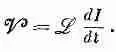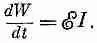Feynmann - Feynmann 6

m 12= m 21= m.

§ 7 . Самоиндукция

При обсуждении индуцированных э. д. с. в двух катушках на фиг. 17.8 и 17.9 мы рассмотрели лишь случай, когда ток проходит либо в одной катушке, либо в другой. Если токи име­ются одновременно в обеих катушках, то магнитный поток, пронизывающий каждую катушку, будет представлять сумму двух потоков, существующих и по отдельности, поскольку к магнитным полям применим принцип суперпозиции. Поэтому э. д. с. в каждой катушке будет пропорциональна не только изменению тока в другой катушке, но и изменению тока в ней самой.

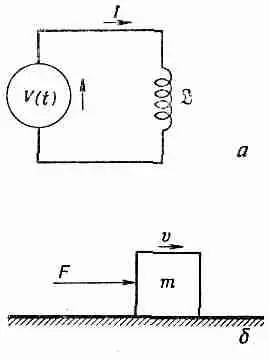
Фиг. 17.10. Цепь с источником напряжения и индуктивностью (а) и аналогичная ей механиче­ская система (б).

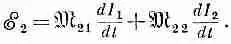
Таким образом, полную э. д. с. в катушке 2 следует за­писать в виде

(17.31)

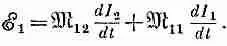
""Аналогично, э. д. с. в катушке 1 будет зависеть не только от изменяющегося тока в катушке 2, но и от изменяющегося тока в ней самой:

(17.32)

Коэффициенты m 22и m 11всегда отрицательны. Обычно пишут

(17.33)

где ж 1и ж 2 называют коэффициентами самоиндукции двух катушек (или индуктивностями).

Конечно, э. д. с. самоиндукции будет существовать даже для одной катушки. Любая катушка сама по себе обладает коэффициентом самоиндукции ж и ее

э. д. с. будет пропорцио­нальна скорости изменения тока в катушке. Обычно считают, Что э. д. с. и ток одной катушки положительны, если они на­правлены одинаково. При этом условии для отдельной катушки

можно написать

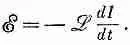
(17.34)

Знак минус указывает на то, что э. д. с. противодействует изменению тока, ее часто называют «обратной э. д. с.».

Поскольку любая катушка обладает самоиндукцией, проти­водействующей изменению тока, ток в катушке обладает своего рода инерцией. Действительно, если мы хотим изменить ток в катушке, мы должны преодолеть эту инерцию, присоединяя катушку к какому-то внешнему источнику, например батарее или генератору (фиг. 17.10, а). В такой цепи ток / связан с на­пряжением V соотношением

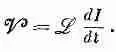
(17.35)

Это соотношение имеет форму уравнения движения Ньютона для частицы в одном измерении. Поэтому мы можем исследо­вать его по принципу «одинаковые уравнения имеют одинако­вые решения». Таким образом, если поставить в соответствие напряжение V от внешнего источника приложенной внешней силе F , а ток I в катушке скорости v частицы, то коэффициент индукции катушки ж будет соответствовать массе т частицы (фиг. 17,10, б).

Таблица 17.1 · СОПОСТАВЛЕННЫЕ ВЕЛИЧИНЫ

§ 8. Индуктивность и магнитная энергия

Продолжая аналогию предыдущего параграфа, мы отметили в таблице, что в соответствии с механическим импульсом p = mv (скорость изменения которого равна приложенной силе) должна существовать аналогичная величина, равная

ж I, ско­рость изменения которой V. Разумеется, мы не имеем права говорить, что ж I — это настоящий импульс цепи; на самом деле это вовсе не так. Вся цепь может быть неподвижна и вооб­ще не иметь импульса. Просто ж I аналогично импульсу mv в смысле удовлетворения аналогичным уравнениям.

Точно так же кинетической энергии 1/ 2mv 2здесь соответствует анало­гичная величина 1/ 2ж 2. Но здесь нас ждет сюрприз. Величина 1/ 2aж I 2— действительно есть энергия и в электрическом случае. Так получается потому, что работа, совершаемая в единицу времени над индуктивностью, равна VI , а в механической систе­ме она равна Fv — соответствующей величине. Поэтому в слу­чае энергии величины не только соответствуют друг другу в математическом смысле, но имеют еще и одинаковое физиче­ское значение.

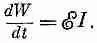
Мы можем проследить это более подробно. В (17.16) мы наш­ли, что электрическая работа в единицу времени за счет сил индукции есть произведение э. д. с. и тока: