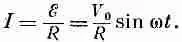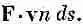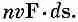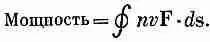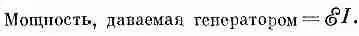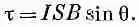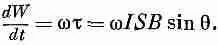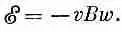Поскольку между проводами имеется электрическое поле, они должны быть электрически заряжены. Ясно, что э. д. с. генератора выталкивает лишние заряды в провода, пока их электрическое поле не становится достаточно сильным, чтобы в точности уравновесить силу индукции. Если посмотреть на генератор со стороны, то покажется, будто два провода электростатически заряжены до разности потенциалов V , а заряды как бы меняются со временем, создавая переменную разность потенциалов. Есть и еще одно отличие от того, что наблюдается в случае электростатики. Если присоединить генератор к внешней цепи, по которой может проходить ток, мы обнаружим, что э. д. с. не позволяет проводам разряжаться, а продолжает подпитывать их зарядами, когда из них уходит ток, стремясь сохранить на проводах одну и ту же разность потенциалов. Если генератор подключен к цепи, полное сопротивление которой равно R , ток в цепи будет пропорционален э. д. с. генератора и обратно пропорционален R . Поскольку э. д. с. синусоидально изменяется со временем,
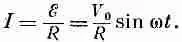
то и ток делает то же самое. Возникает переменный ток
Схема такой цепи приведена на фиг. 17.7.
Мы можем также заметить, что э. д. с. определяет количество энергии, поставляемое генератором. Каждый заряд в проводе получает в единицу времени энергию, равную F·v, где F — сила, действующая на заряд, a v — его скорость. Пусть теперь количество движущихся зарядов на единице длины провода равно n ; тогда мощность, выделяющаяся в элементе ds провода, равна
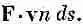
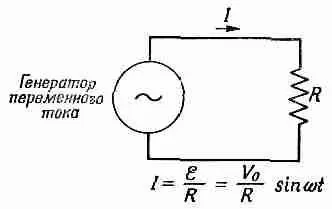
Фиг. 17.7. Цепь с генератором переменного тока и сопротивлением.
В проводе скорость v всегда направлена вдоль ds , так что мощность можно переписать в виде
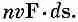
Полная мощность, выделяемая во всей цепи, есть интеграл от этого выражения по всей петле:
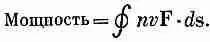
(17.15)
Вспомним теперь, что qnv — это ток I и что э. д. с. определяется как интеграл от F / q по всей цепи. Мы получаем
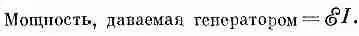
(17.16)
Когда в катушке генератора имеется ток, на нее непременно действуют механические силы. В самом деле, мы знаем, что вращающий момент, действующий на катушку, пропорционален ее магнитному моменту, напряженности магнитного поля В и синусу угла между ними. Магнитный момент есть ток катушки, умноженный на ее площадь. Поэтому вращающий момент равен
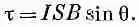
(17.17)
Скорость, с которой должна совершаться механическая работа, чтобы поддерживать вращение катушки, есть угловая скорость w, умноженная на вращающий момент силы:
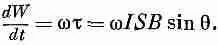
(17.18)
Сравнивая это выражение с (17.14), мы видим, что затраты механической работы в единицу времени, требуемые для вращения катушки против магнитных сил, в точности равны e I — электрической энергии, поставляемой
э. д. с. генератора в единицу времени. Вся механическая энергия, расходуемая в генераторе, появляется в виде электрической энергии в цепи.
В качестве другого примера токов и сил, обусловленных индуцированной э. д. с., проанализируем, что же происходит в установке, показанной на фиг. 17.1. Имеются U-образная проволока и скользящая перемычка, расположенные в однородном магнитном поле, перпендикулярном плоскости параллельных проволок. Теперь предположим, что «дно» U (левая часть фиг. 17.1) сделано из проволоки с большим сопротивлением, тогда как две боковые проволоки сделаны из хорошего проводника вроде меди — в этом случае нам не надо беспокоиться об изменении сопротивления цепи при движении перекладины. Как и раньше,
э. д. с. цепи равна
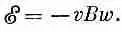
Читать дальше