Feynmann - Feynmann 6

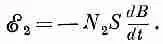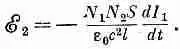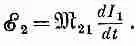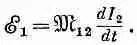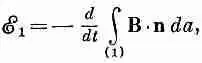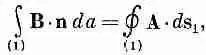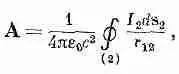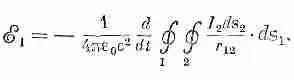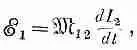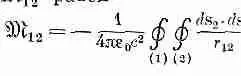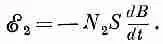
.(17.24)

Единственная меняющаяся со временем величина в (17.23) есть I 1. Поэтому э. д. с. дается выражением

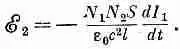
(17.25)

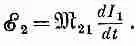
Мы видим, что э. д. с. в катушке 2 пропорциональна скорости изменения тока в катушке 1. Константа пропорциональности — по существу геометрический фактор двух катушек, называется коэффициентом взаимной индукции и обозначается обычно m 21. Тогда (17.25) записывается уже в виде

(17.26)

Предположим теперь, что нам нужно было бы пропустить ток через катушку 2 и нас интересует, чему равна э. д. с. в ка­тушке 1. Мы вычислили бы магнитное поле, которое повсюду пропорционально току I 2. Поток сквозь катушку I зависел бы от геометрии, но был бы пропорционален току I 2. Поэтому

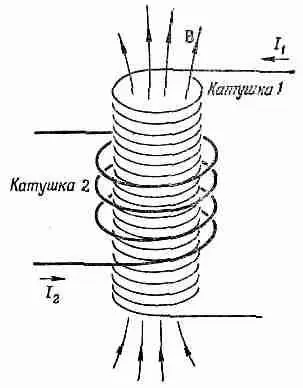
Фиг. 17.8. Ток в катушке 1 соз­дает магнитное поле, проходящее через катушку 2.

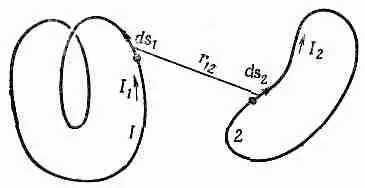
Фиг. 17.9. Любые две катушки обладают взаимной индукцией m , пропорциональной инте­гралу от ds 1 · ds 2 · (1/ r 12 ).

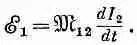
э. д. с. в катушке 1 снова была бы пропорциональна dI 2 / dt . Мы можем записать

(17.27)

Вычисление m 12было бы труднее, чем те вычисления, кото­рые мы проделали для m 21. Мы не будем сейчас им заниматься, потому что дальше в этой главе мы покажем, что m 12обя­зательно равно m 21 .

Поскольку поле любой катушки пропорционально текущему в ней току, такой же результат получился бы и для любых двух катушек из проволоки. Выражения (17.26) и (17.27) при­обрели бы одинаковую форму, и только постоянные m 12и m 21были бы другие. Их значения будут зависеть от формы кату­шек и их относительного положения.

Предположим, нам нужно найти коэффициент взаимной ин­дукции между двумя произвольными катушками, например показанными на фиг. 17.9. Мы знаем, что общее выражение для э. д. с. в катушке 1 можно записать так:

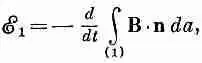
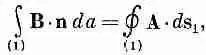
где В — магнитное поле, а интеграл берется по поверхности, ограниченной контуром 1 . В гл. 14, § 1 (вып. 5) мы видели, что поверхностный интеграл от В можно свести к контурному ин­тегралу от векторного потенциала. В нашем случае

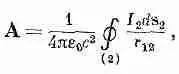
как контурный интеграл по контуру цепи 2:

(17.29)

где I 2— ток в цепи 2, а r 12— расстояние от элемента цепи ds 2 к точке на контуре 1 , в которой мы вычисляем векторный потенциал (см. фиг. 17.9). Комбинируя (17.28) и (17.29), можно выразить э. д. с. в цепи 1 как двойной контурный интеграл:

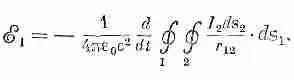
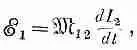
В этом выражении все интегралы берутся по неподвижным кон­турам. Единственной переменной величиной является ток I 2, который не зависит от переменных интегрирования. Поэтому его можно вынести за знак интеграла. Тогда э. д. с. можно записать как

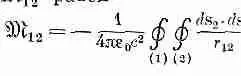
где коэффициент m 12равен

(17.30)

Из этого интеграла очевидно, что m 12зависит только от гео­метрии цепей; он зависит от некоторого среднего расстояния между двумя цепями, причем в среднее с наибольшим весом входят параллельные отрезки проводников двух катушек. Нашу формулу можно использовать для вычисления коэффи­циента взаимной индукции любых двух цепей произвольной формы. Кроме того, она показывает, что интеграл для m 12тождествен с интегралом для m 21. Таким образом, мы показали, что оба коэффициента одинаковы. Для системы только с двумя катушками коэффициенты m 12и m 21часто обозначают символом m без значков и называют просто коэффициентом взаимной индукции: