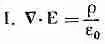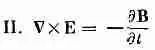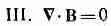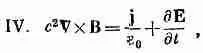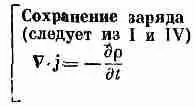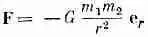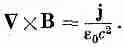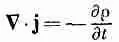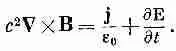Feynmann - Feynmann 6

Уравнения Максвелла

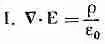
(Поток Е через замкнутую поверх­ность) = (Заряд внутри нее)/e 0

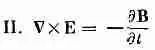
(Интеграл от Е по замкнутому кон­туру) = -d/dt (Поток В сквозь контур)

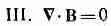
(Поток В через замкнутую поверх­ность) = 0

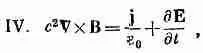
с 2(Интеграл от В по контуру)=(Ток в контуре) /e 0+ d/dt(Поток Е сквозь контур)

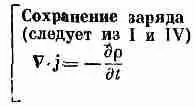
(Поток заряда через замкнутую по­верхность) =-d/dt(Заряд внутри нее)

Закон силы

F = q(E+vXB)

Закон движения

(Закон Ньютона, исправлен­ный Эйнштейном}

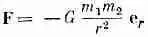
Гравитация

Поскольку магнитных зарядов нет, поток В через любую замкнутую поверхность всегда равен нулю. Второе уравнение СXE=- dB / dt — это закон Фарадея, и обсуждался он в последних двух главах. Он тоже верен в общем случае. Но последнее уравнение содержит нечто новое. Раньше мы встречались только с частью его, которая годится для постоянных токов. В этом случае мы говорили, что ротор В равен j/e 0c 2, но правильное общее уравнение имеет новый член, который был открыт Максвеллом.

До появления работы Максвелла известные законы элек­тричества и магнетизма были такими же, как те, что мы изучали в гл. 3—14 (вып. 5) и гл. 15—17. В частности, урав­нение для магнитного поля постоянных токов было известно только в виде

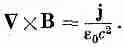
(18.1)

Максвелл начал с рассмотрения этих известных законов и вы­разил их в виде дифференциальных уравнений, так же как мы поступили здесь. (Хотя символ С еще не был придуман, впер­вые, в основном благодаря Максвеллу, стала очевидной важ­ность таких комбинаций производных, которые мы сегодня называем ротором и дивергенцией.) Максвелл тогда заметил, что в уравнении (18.1) есть нечто странное. Если взять дивер­генцию от этого уравнения, то левая сторона обратится в нуль, потому что дивергенция ротора всегда равна нулю. Таким об­разом, это уравнение требует, чтобы дивергенция j также была равна нулю. Но если дивергенция j равна нулю, то полный ток через любую замкнутую поверхность тоже равен нулю.

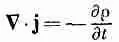
Полный ток через замкнутую поверхность равен уменьше­нию заряда внутри этой поверхности. Он наверняка не может быть всегда равен нулю, так как мы знаем, что заряды могут перемещаться из одного места в другое. Уравнение

(18.2)

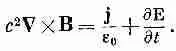
фактически есть наше определение j. Это уравнение выражает самый фундаментальный закон — сохранение электрического заряда: любой поток заряда должен поступать из какого-то запаса. Максвелл заметил эту трудность и, чтобы избежать ее, предложил добавить dE / dt в правую часть уравнения (18.1); тогда он и получил уравнение IV в табл. 18.1:

Во времена Максвелла еще не привыкли мыслить в терми­нах абстрактных полей. Максвелл обсуждал свои идеи с по­мощью модели, в которой вакуум был подобен упругому телу. Он пытался также объяснить смысл своего нового уравнения с помощью механической модели. Теория Максвелла принималась очень неохотно, во-первых, из-за модели, а, во-вторых, потому, что вначале не было экспериментального подтверждения. Сей­час мы лучше понимаем, что дело в самих уравнениях, а не в модели, с помощью которой они были получены. Мы можем только задать вопрос, правильны ли эти уравнения или они ошибочны. Ответ дает эксперимент. И уравнения Максвелла были подтверждены в бессчетных экспериментах. Если мы отбросим все строительные леса, которыми пользовался Мак­свелл, чтобы построить уравнения, мы придем к заключению, что прекрасное здание, созданное Максвеллом, держится само по себе. Он свел воедино все законы электричества и магне­тизма и создал законченную и прекрасную теорию.

Давайте покажем, что добавочный член имеет тот самый вид, который требуется, чтобы преодолеть обнаруженную Мак­свеллом трудность. Взяв дивергенцию его уравнения (IV в табл. 18.1), мы должны получить, что дивергенция правой части равна нулю: