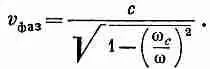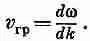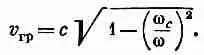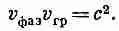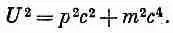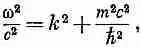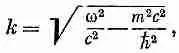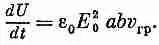Feynmann - Feynmann 6a

что можно также представить в виде

(24.24)

Это выражение приводит к полю Е, которое во времени колеб­лется как e i w t , a no z меняется как e ± k ' z . Оно плавно убывает или возрастает с z, как всякая действительная экспонента. В нашем выводе мы не думали о том, откуда взялись волны, где их источник, но, конечно, где-то в волноводе он должен быть. И знак, который стоит при k ' , должен быть таков, чтобы поле убывало при удалении от источника волн.

Итак, при частотах ниже w с — p с/а волны вдоль трубы не рас­пространяются; осциллирующее поле проникает в трубу лишь на расстояние порядка i / k ' . По этой причине частоту w с назы­вают «граничной частотой» волновода. Глядя на (24.22), мы ви­дим, что для частот чуть пониже w cчисло k ' мало, и поля могут проникать в трубу довольно далеко. Но если со намного меньше w с, коэффициент k ' в экспоненте равняется p/а, и поле отмирает чрезвычайно быстро (фиг. 24.7). Поле убывает в е раз на расстоя­нии а/p, т. е. на трети ширины волновода. Поля проникают в волновод на очень малое расстояние от источника.

Мы хотим еще раз подчеркнуть эту характерную черту на­шего анализа прохождения волн по трубе — появление мнимого волнового числа k z . Когда, решая уравнение в физике, мы полу­чаем мнимое число, то это обычно ничего физического не озна­чает. Для волн, однако, мнимое волновое число действительно нечто означает. Волновое уравнение по-прежнему удовлетво­ряется; оно только означает, что решение приводит к экспоненциально убывающему полю вместо распространяющихся волн

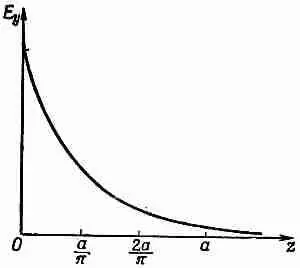
Фиг. 24.7. Изменение Е y с ро­стом z при w

Итак, если в любой задаче на волны k при какой-то частоте ста­новится мнимым, это означает, что форма волны меняется — синусоида переходит в экспоненту.

§ 4. Скорость волн в волноводе

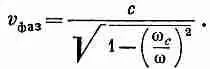
Та скорость волн, о которой мы пока говорили,— это фа­зовая скорость, т. е. скорость узлов волны; она есть функция частоты. Если подставить (24.17) в (24.18), то можно написать

(24.25)

Для частот выше граничной (для которых бегущая волна суще­ствует) w c/w меньше единицы, v фаз— действительное число, боль­шее скорости света. Мы уже видели в гл. 48 (вып. 4), что фазовые скорости, большие скорости света, возможны, потому что это просто движутся узлы волн, а не энергия и не информация. Чтобы узнать, как быстро движутся сигналы, надо подсчитать быстроту всплесков или модуляций, вызываемых интерферен­цией волн одной частоты с одной или несколькими волнами слегка иных частот [см. гл. 48 (вып. 4)]. Скорость огибающей такой группы волн мы назвали волновой скоростью; это не w/k, a d w / dk :

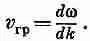
(24.26)

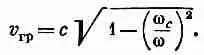
Дифференцируя (24.17) по w и переворачивая, чтобы полу­чить d w / dk , получаем

(24.27)

Это меньше скорости света.

Среднее геометрическое между v фаз и v грв точности равно с — скорости света:

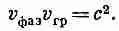
(24.28)

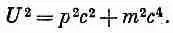
Это любопытно, ведь сходное соотношение мы встречали и в квантовой механике. У частицы с любой скоростью (даже у релятивистской) импульс р и энергия U связаны соот­ношением

(24.29)

Но в квантовой механике энергия — это hw, а импульс —это h / l ’ , или h k ; значит, (24.29) можно записать так:

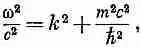
(24.30)

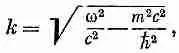
или

(24.31)

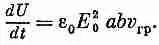
а это очень похоже на (24.17). . . Интересно, не правда ли? Групповая скорость волн — это также скорость, с какой энергия передается по трубе. Если вам нужно найти поток энер­гии сквозь волновод, надо умножить плотность энергии на груп­повую скорость. Если среднее квадратичное электрическое поле равно Е 0 , то средняя плотность электрической энергии равна e 0 Е 2 0 /2. Кроме этого, часть энергии связана с магнитным полем. Мы не будем здесь это доказывать, но в любой полости или трубе магнитная и электрическая энергии равны между собой, так что полная плотность электромагнитной энергии равна e 0 Е 2 0 . А мощность dU / dt , передаваемая волноводом, поэтому равна