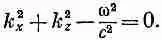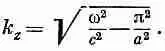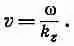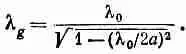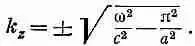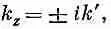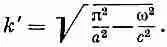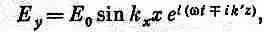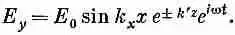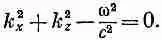
Если Е y не обращается всюду в нуль (этот случай нас не очень интересует), то это уравнение выполняется всегда, если
(24.16)
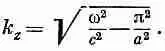
Число k x мы уже закрепили, так что это уравнение говорит нам, что волны предположенного нами типа возможны лишь тогда, когда k z связано с частотой w условием (24.16), т. е. когда
(24.17)
Волны, которые мы описали, распространяются в направлении z с таким значением k z .
Волновое число k z, которое мы получили из (24.17), дает нам при данной частоте w скорость, с которой бегут вдоль трубы узлы волны. Фазовая скорость равна
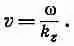
(24.18)
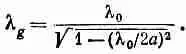
Вспомните теперь, что длина l, бегущей волны дается формулой l =2 p v / w , так что k z также равняется 2 p / l g , где l g — длина волны осцилляции в направлении z — «длина волны в волноводе». Длина волны в волноводе, конечно, отличается от длины электромагнитных волн той же частоты, но в пустом пространстве. Если длину волны в пустом пространстве обозначить l 0(что равно 2 p с/w), то (24.17) можно переписать в таком виде:
(24.19)
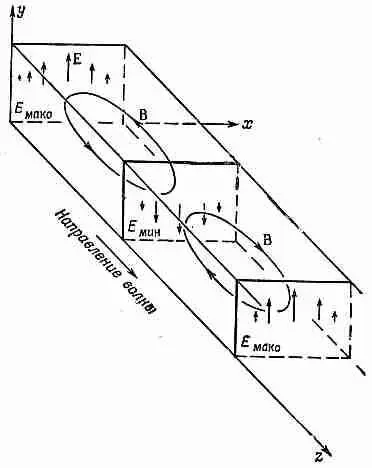
Фиг. 24 . 6. Магнитное поле в волноводе.
Кроме электрических полей, существуют и магнитные поля, которые тоже движутся волнообразно. Мы не будем сейчас заниматься выводом выражений для них. Ведь c 2СXВ = dE / dt , и линии В циркулируют вокруг областей, где dE / dt — наибольшее, т. е. на полпути между максимумом и минимумом Е. Петли В лежат параллельно плоскости xz и между гребнями и впадинами Е (фиг. 24.6).
§ 3. Граничная частота
Уравнение (24.16) для k zна самом деле имеет два корня — один с плюсом, другой с минусом. Ответ следует писать так:
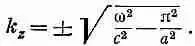
(24.20)
Смысл этих двух знаков просто в том, что волны в волноводе могут бежать и с отрицательной фазовой скоростью (в направлении —z), и с положительной. Волны, естественно, должны иметь возможность бежать в любую сторону. И раз одновременно могут существовать оба типа волн, то решение в виде стоячих волн тоже возможно.
Наше уравнение для k z сообщает нам также, что высшие частоты приводят к большим значениям k g , т. е. к более коротким волнам, пока в пределе больших w величина k не станет равной w/с — тому значению, которое бывает, когда волна бежит в пустоте. Свет, который мы «видим» сквозь трубу, все еще бежит со скоростью с. Но посмотрите зато, какая странная вещь получается, когда частота убывает. Сперва волны становятся все длиннее и длиннее. Но если частота w станет чересчур малой, то под корнем в (24.20) внезапно появится отрицательное число. Это произойдет, когда w перевалит через pс/а или когда l 0станет больше 2а. Иначе говоря, когда частота становится меньше некоторой критической частоты w c=pс/а, волновое число k z (а также l g ) становится мнимым и никакого решения у нас не остается. Или остается? Кто, собственно, сказал, что k z должно быть действительным? Что случится, если оно станет мнимым? Уравнения-то поля по-прежнему ведь будут удовлетворяться. Может быть, и мнимые k z тоже представляют какую-то волну?
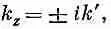
Предположим, что w действительно меньше w c; тогда можно написать
(24.21)
где k ' — действительное положительное число
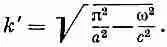
(24.22)
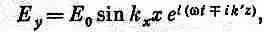
Если теперь вернуться к нашей формуле (24.12) для Е y , то надо будет написать
(24.23)
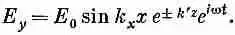
Читать дальше