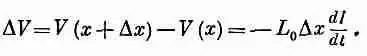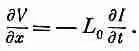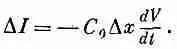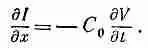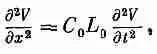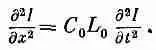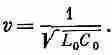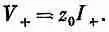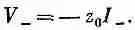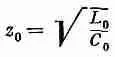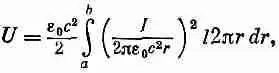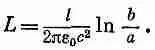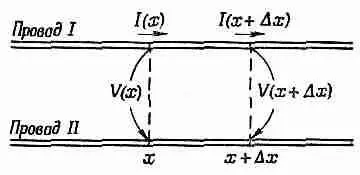
Фие. 24.2. Токи и напряжения в передающей линии.
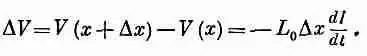
Предположим, мы наблюдаем за происходящим в двух соседних точках передающей линии, скажем, на расстояниях х и х+Dх от начала линии. Обозначим напряжение между проводниками через V(x), а ток в верхнем проводнике I(х} (фиг. 24.2). Если ток в линии меняется, то индуктивность вызовет падение напряжения вдоль небольшого участка линии от х до x+Dx
Или, беря предел при D x ® 0 , получаем
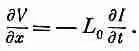
(24.1)
Изменение тока приводит к перепаду напряжения.
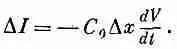
Теперь еще раз взгляните на рисунок. Если напряжение в х меняется, то должны появляться заряды, которые на этом участке передаются емкости. Если взять небольшой участок линии от х до x+Dx, то заряд на нем равен q = C 0DxV. Скорость изменения этого заряда равна C 0DxdV/dt, но заряд меняется только тогда, когда ток I(х), входящий в элемент, отличается от выходящего тока I(х+Dх), Обозначая разность через DI,
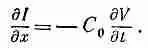
Если перейти к пределу при Dx®0, получается
(24.2)
Так что сохранение заряда предполагает, что градиент тока пропорционален скорости изменения напряжения во времени. Уравнения (24.1) и (24.2) — это основные уравнения линии передачи. При желании их можно видоизменить так, чтобы они учитывали сопротивление проводников или утечку зарядов через изоляцию между проводниками, но пока нам достаточно самого простого примера.
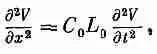
Оба уравнения передающей линии можно объединить, продифференцировав первое по t, а второе по x; и исключив V или I. Получится либо
(24.3)
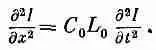
либо
(24.4)
Мы снова узнаем волновое уравнение по х. В однородной передающей линии напряжение (и ток) распространяется вдоль линии как волна. Напряжение вдоль линии будет следовать закону V(x, t)=f(x-vt) или V(x, t)=g(x+vt) или их сумме. А что такое здесь v? Мы знаем, что коэффициент при d 2/dt 2— это просто 1/v 2. так что
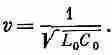
(24.5)
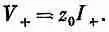
Покажите самостоятельно, что напряжение для каждой волны в линии пропорционально току этой волны и что коэффициент пропорциональности — это просто характеристический импеданс z 0. Обозначив через V +и I +напряжение и ток для волны, бегущей в направлении +x, вы должны будете получить
(24.6)
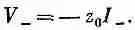
Равным образом, для волны, бегущей в направлении -х, получится
Характеристический импеданс, как мы уже видели из наших уравнений для фильтра, дается выражением
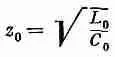
(24.7)
и поэтому есть чистое сопротивление.
Чтобы найти скорость распространения v и характеристический импеданс z 0передающей линии, нужно знать индуктивность и емкость единицы длины линии. Для коаксиального кабеля их легко подсчитать. Поглядим, как это делается. При расчете индуктивности мы будем следовать идеям, изложенным в гл. 17, § 8, и положим 1/ 2 LI 2 равным магнитной энергии, в свою очередь получаемой интегрированием e 0с 2B 2/2 по объему. Пусть по внутреннему проводнику течет ток I; тогда мы знаем, что B=I/2pe 0с 2r, где r — расстояние от оси. Беря в качестве элемента объема цилиндрический слой толщины dr и длины l ,
получаем для магнитной энергии
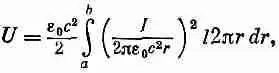

где а и b — радиусы внутреннего и внешнего проводников, Интегрируя, получаем
(24.8)
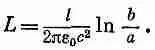
Читать дальше