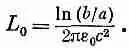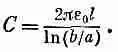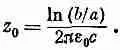Feynmann - Feynmann 6a

Приравниваем эту энергию к 1 I 2 LI 2 и находим

(24.9)

Как и следовало ожидать, L пропорционально длине l линии, поэтому L 0 (индуктивность на единицу длины) равна

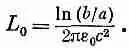
(24.10)

Мы уже рассчитывали заряд на цилиндрическом конден­саторе [гл. 12, § 2 (вып. 5)]. Деля теперь этот заряд на раз­ность потенциалов, получаем

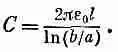
Емкость же на единицу длины С 0 — это С/ l . Сопоставляя этот результат с (24.10), мы убеждаемся, что произведение L 0 C 0 равно просто 1/с 2, т. е. v =1 Ц L 0 C 0 равно с. Волна бежит по линии со скоростью света. Нужно подчеркнуть, что этот результат зави­сит от сделанных предположений: а) что в промежутке между проводниками нет ни диэлектриков, ни магнитных материалов; б) что все токи текут только по поверхности проводников (как это бывает в идеальных проводниках). Позже мы увидим, что на высоких частотах все токи распределяются на поверхности хоро­ших проводников, словно они идеальные проводники, так что это предположение правильно.

Любопытно, что в этих двух предположениях произведение L 0 C 0 равно 1 /с 2 для любой параллельной пары проводников, да­же в том случае, если, скажем, внутренний шестигранный про­водник тянется как-то вдоль эллиптического внешнего. Пока сечение постоянно и между проводниками нет ничего, волны рас­пространяются со скоростью света.

Подобных общих утверждений по поводу характеристиче­ского импеданса сделать нельзя. Для коаксиальной линии он равен

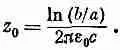
(24.11)

Множитель 1/e 0c имеет размерность сопротивления и равен 120p ом. Геометрический фактор In(b/a) только логарифмически зависит от размеров, так что коаксиальная линия (и большинст­во других линий), как правило, обладает характеристическим импедансом порядка 50 ом или что-то около этого, до нескольких сот ом.

§ 2. Прямоугольный волновод

То, о чем мы сейчас будем говорить, на первый взгляд ка­жется поразительным явлением: если из коаксиального кабеля убрать внутреннюю жилу, он все равно будет проводить элект­ромагнитную энергию. Иными словами, на достаточно высокой частоте полая труба действует ничуть не хуже, чем труба, внут­ри которой имеется провод. Связано это с другим таинственным явлением, о котором мы уже знаем,— на высоких частотах ре­зонансный контур (конденсатор с катушкой) можно заменить простой банкой.

Это выглядит очень странно, если пользоваться представле­нием о передающей линии, как о распределенных индуктивности и емкости. Но ведь все мы знаем, что внутри пустой металличе­ской трубы могут распространяться электромагнитные волны. Если труба прямая, через нее все видно! Значит, электромаг­нитные волны через трубу бесспорно проходят. Но мы знаем также, что нет возможности передавать волны низкой частоты (переменный ток или телефонные сигналы) через одну-единственную металлическую трубу. Выходит, электромагнитные вол­ны проходят через нее только тогда, когда их длина волны дос­таточно мала. Поэтому мы рассмотрим предельный случай самых длинных волн (или самых низких частот), способных про­ходить через трубу данного размера. Эту трубу, служащую для прохождения волн, называют волноводом.

Начнем с прямоугольной трубы, ее проще всего анализи­ровать. Сперва изложим все математически, а потом еще раз вернемся назад и рассмотрим вопрос более элементарно. Но этот более элементарный подход легко применить лишь к прямо­угольным трубам. Основные же явления в любой трубе одни и те же, так что математические доводы звучат более основа­тельно.

Поставим перед собой следующий вопрос: какого типа волны могут существовать в прямоугольной трубе? Выберем сначала удобные оси координат: ось z направим вдоль трубы, а оси х и у — вдоль стенок (фиг. 24.3).

Известно, что когда волны света бегут по трубе, их электри­ческое поле поперечно; поэтому начнем с поиска таких решений, в которых Е перпендикулярно z, скажем решений с одной толь­ко y-компонентой Е y(фиг. 24.4,а). Это электрическое поле должно как-то меняться поперек волновода; действительно, ведь оно должно обратиться в нуль на сторонах, параллельных оси у: токи и заряды в проводнике устраиваются всегда так, чтобы на его поверхности не осталось никаких касательных составляющих электрического поля.