Feynmann - Feynmann 5

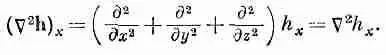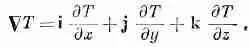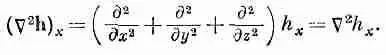
(2.60)

Ио это выражение не годится, если мы ищем радиальную ком­поненту С 2h. Она не равна С 2h r. Дело в том, что в алгебре век­торов все их направления полностью определены. А когда мы имеем дело с векторными полями, то их направления в разных местах различны. Когда мы пробуем описать векторное поле, например, в полярных координатах, то «радиальное» направле­ние меняется от точки к точке. И начав дифференцировать ком­поненты, вы запросто можете попасть в беду. Даже в постоян­ном векторном поле радиальная компонента от точки к точке меняется.

Обычно безопаснее и проще всего держаться прямоугольных координат. Но стоит упомянуть и одно исключение: поскольку лапласиан С 2есть скаляр, то можно писать его в любой системе координат (скажем, в полярных координатах). Но так как это дифференциальный оператор, то применять его надо только к векторам с фиксированным направлением компонент, т. е. к заданным в прямоугольных координатах. Итак, расписывая наши векторные дифференциальные уравнения покомпонентно, мы будем предварительно выражать все наши векторные поля через их х-, у-, z-компоненты.

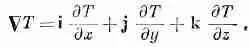
* В наших обозначениях выражение (а, b , с) представляет вектор с компонентами а, b , с. Если вам нравится пользоваться единичными векторами i , j и k , то можно написать

* Мы рассматриваем h как физическую величину, зависящую от по­ложения в пространстве, а не как заданную математически функцию трех переменных. Когда h «дифференцируется» по х, у и z или по х', у' и z ', то математическое выражение для h должно быть предварительно выраже­но в виде функции соответствующих переменных, Поэтому в новой си­стеме координат мы не отмечаем h штрихом.

Глава 3

ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ВЕКТОРОВ

§1.Векторные интег­ралы; криволи­нейный интеграл от ▽ ш

§2.Поток векторного поля

§З. Поток из куба; теорема Гаусса

§4.Теплопроводность; уравнение диффу­зии

§5.Циркуляция векторного поля

§6. Циркуляция по квадрату; теорема Стокса

§7. Поля без роторов и поля без дивер­генций

§8.Итоги

§ 1. Векторные интегралы;

криволинейный интеграл от С ш

В предыдущей главе мы видели, что брать производные от поля можно по-разному. Одни приводят к векторным полям; другие — к скалярным. Хотя формул было выведено до­вольно много, все их можно подытожить одним правилом: операторы д/дх, д/ду и д / dz суть три компоненты векторного оператора у. Сейчас нам хотелось бы лучше разобраться в значении производных поля. Тогда мы легче почувствуем смысл векторных уравнений поля.

Мы уже говорили о смысле операции градиен­та (С на скаляр). Обратимся теперь к смыслу опе­раций вычисления дивергенции (расходимости) и ротора (вихря). Толкование этих величин лучше всего сделать на языке векторных интегралов и уравнений, связывающих эти интегралы. Но уравнения эти, к несчастью, нельзя вывести из векторной алгебры при помощи каких-либо легких подстановок, так что вам придется учить их как что-то новое. Одна из этих инте­гральных формул практически тривиальна, а другие две — нет. Мы выведем их и поясним их смысл. Эти формулы фактически являются математическими теоремами. Они полезны не только для толкования смысла и содержания понятий дивергенции и ротора, но и при раз­работке общих физических теорий. Для теории полей эти математические теоремы — все равно, что теорема о сохранении энергии для меха­ники частиц. Подобные теоремы общего харак­тера очень важны для более глубокого пони­мания физики. Но вы увидите, что, за немногими простыми исключениями, они мало что дают для решения задач. К счастью, как

раз в начале нашего курса многие простые задачи будут решаться именно этими тремя интегральными формулами.