Feynmann - Feynmann 5

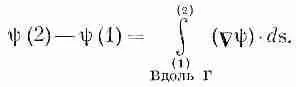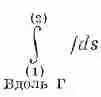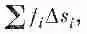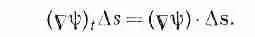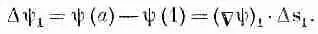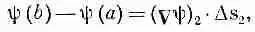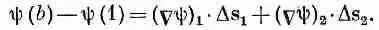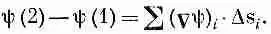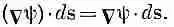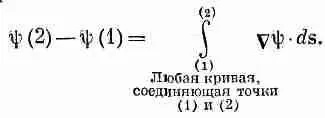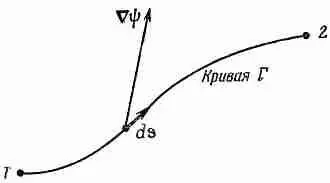
Фиг. 3.1. Иллюстрация уравнения (3.1).

Вектор С ш вычисляется на линей­ном элементе ds .

Позже, однако, когда задачи станут потруднее, этими простыми методами мы больше обойтись не сможем.

Мы начнем с той интегральной формулы, куда входит гра­диент. Мысль, которая содержится в ней, очень проста: раз градиент есть быстрота изменения величины поля, то интеграл от этой быстроты даст нам общее изменение поля. Пусть у нас есть скалярное поле ш ( x , у, z). В двух произвольных точках (1) и (2) функция я|з имеет соответственно значения ш(l) и ш(2). [Используется такое удобное обозначение: (2) означает точку (x 2, y 2, z 2), а ш(2) это то же самое, что ш(x 2, y 2, z 2).] Если Г (гамма) — произвольная кривая, соединяющая (1) и (2) (фиг. 3.1), то справедлива

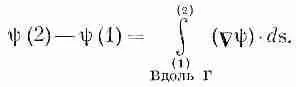
Т Е О Р Е М А 1

(3.1)

Интеграл, стоящий здесь, это криволинейный интеграл от (1) до (2) вдоль кривой Г от скалярного произведения вектора Сш) на другой вектор, ds , являющийся бесконечно малым элемен­том дуги кривой Г [направленной от (1) к (2)].

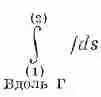
Напомним, что мы понимаем под криволинейным интегралом. Рассмотрим скалярную функцию f(x, y, z) и кривую Г, соеди­няющую две точки (1) и (2). Отметим на кривой множество то­чек и соединим их хордами, как на фиг. 3.2. Длина i-й хорды равна Ds i,-, где i пробегает значения 1, 2, 3, .... Под криволиней­ным интегралом

подразумевается предел суммы

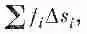
где f i— значение функции где-то на i-й хорде. Предел — это то,

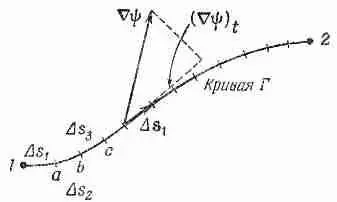
Фиг. 3.2. Криволинейный интег­рал есть предел суммы.

к чему стремится сумма, когда растет число хорд (разумным об­разом, чтобы даже наибольшее Ds i®0).

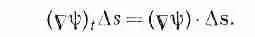
В нашей теореме (3.1) интеграл означает то же самое, хоть и выглядит чуть по-иному. Вместо f стоит другой скаляр — составляющая Сш в направлении Ds. Если обозначить эту составляющую через (Сш) t , то ясно, что

(3.2)

Интеграл в (3.1) и подразумевает сумму таких членов.

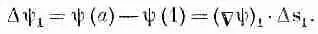
А теперь посмотрим, почему уравнение (3.1) правильно. В гл. 1 мы показали, что составляющая Сш вдоль малого сме­щения DR равна быстроте изменения ш в направлении DR. Рассмотрим хорду кривой Ds от точки (1) до точки а на фиг. 3.2. По нашему определению

(3.3)

Точно так же мы имеем

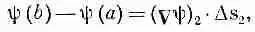
(3.4)

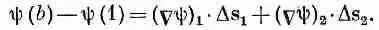
где, конечно, (Сш) 1означает градиент, вычисленный на хорде Ds 1, a (Сш) 2— градиент, вычисленный на Ds 2. Сложив (3.3) и (3.4), получим

(3.5)

Вы видите, что, продолжая прибавлять такие члены, мы полу­чаем в итоге

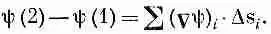
(3.6)

Левая часть не зависит от того, как выбирать интервалы — лишь бы точки (1) и (2) были теми же самыми, так что справа можно перейти к пределу. Так доказывается уравнение (3.1). Из нашего доказательства видно, что, подобно тому как ра­венство не зависит и от выбора точек а, b , с,..., точно так же оно не зависит от выбора самой кривой Г. Теорема верна для любой кривой, соединяющей точки (1) и (2).

Два слова об обозначениях. Не будет путаницы, если писать для удобства

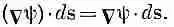
(3.7)

Тогда наша теорема примет такой вид:

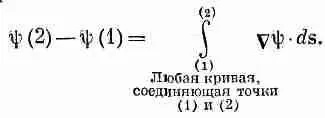
Т Е О Р Е М А 1

(3.8)

§ 2. Поток векторного поля

Прежде чем рассматривать следующую интегральную теоре­му — теорему о дивергенции,— хотелось бы разобраться в од­ной идее, смысл которой в случае теплового потока легко усваи­вается. Мы уже определили вектор h, представляющий коли­чество тепла, протекающего сквозь единицу площади в еди­ницу времени. Положим, что внутри тела имеется замкнутая поверхность S , ограничивающая объем V (фиг. 3.3). Нам хочется узнать, сколько тепла вытекает из этого объема. Мы это можем, конечно, определить, рассчитав общий тепловой поток через поверхность S .