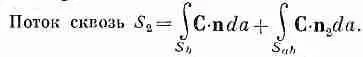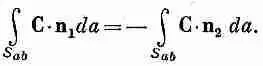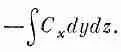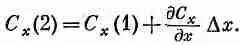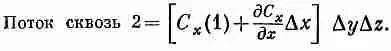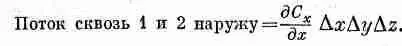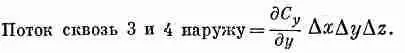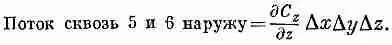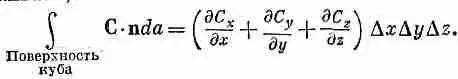Feynmann - Feynmann 5

(3.14)

а для потока из V 2:

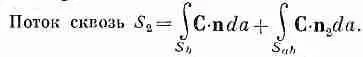
(3.15)

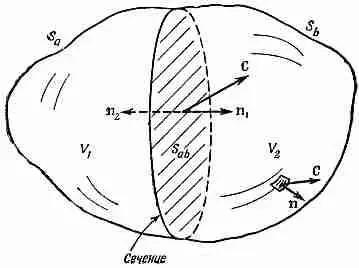
Заметьте, что во втором интеграле мы обозначили внешнюю нормаль к S ab буквой n 1, если она относится к S 1 , и буквой n 2, если она относится к S 1 (см. фиг. 3.4).

Фиг. 3.4. Объем V , заключенный внутри поверхности S , делится на две части «сече­нием» (поверхностью S ab ). Получается объем V 1 , окруженный поверхностью S 1 = S a + S ab , и объем V 2 , окруженный поверхностью S 2 = S b + S ab .

Ясно, что n 1=-n 2, и тем

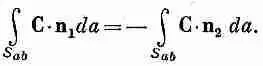
самым

(3.16)

Складывая теперь уравнения (3.14) и (3.15), мы убеждаемся, что сумма потоков сквозь S 1 и S 2 как раз равна сумме двух ин­тегралов, которые, взятые вместе, дают поток через перво­начальную поверхность S = S a + S b .

Мы видим, что поток через всю внешнюю поверхность S можно рассматривать как сумму потоков из тех двух частей, на которые разрезан объем. Эти части можно еще разрезать: скажем, V 1 разбить пополам. Опять придется прибегнуть к тем же доводам. Так что для любого способа разбиения первоначаль­ного объема всегда остается справедливым то свойство, что по­ток через внешнюю поверхность (первоначальный интеграл) равен сумме потоков изо всех внутренних частей.

§ 3. Поток из куба; теорема Гаусса

Рассмотрим теперь частный случай потока из маленького ку­бика и получим интересную формулу. Ребра куба пусть нап­равлены вдоль осей координат (фиг. 3.5), координаты вершины, ближайшей к началу, суть х, у, z, ребро куба в направлении х равно Dx, ребро куба (а точнее, бруска) в направлении у равно Dy, а в направлении z равно Dz. Мы хотим найти поток вектор­ного поля С через поверхность куба. Для этого вычислим сумму потоков через все шесть граней. Начнем с грани 1 (см. фиг. 3.5).

Поток наружу сквозь нее равен x-компоненте С с минусом, проинтегрированной по площади грани. Он равен

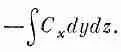
Так как куб считается малым, этот интеграл можно заменить значением С хв центре грани 1эту точку мы обозначили (1), умноженным на площадь грани DyDz:

Поток сквозь 1 наружу=-C x(1)DyDz.

Подобным же образом поток наружу через грань 2 равен

Поток сквозь 2 наружу= C x(2) DyDz.

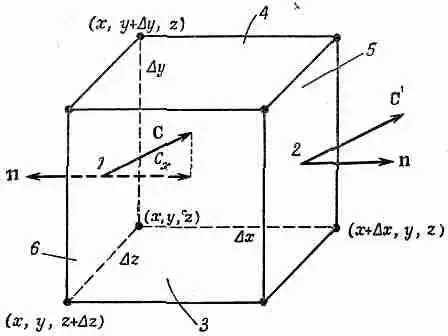
Фиг. 3.5. Вычисление потока вектора С из маленького кубика.

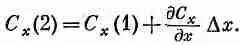
Величины C x (1) и С х (2), вообще говоря, слегка отличаются. Ес­ли Dх достаточно мало, то можно написать

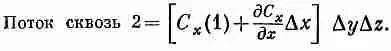
Существуют, конечно, и другие члены, но в них входит (Dx) 2и высшие степени Dx, и в пределе малых Dx ими запросто можно пренебречь. Значит, поток сквозь грань 2 равен

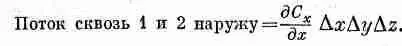
Складывая потоки через грани 1 и 2, получаем

Производную нужно вычислять в центре грани 1, т. е. в точке [ x ,y+(Dy/2), z+(Dz/2)]. Но если куб очень маленький, мы сде­лаем пренебрежимую ошибку, если вычислим ее в вершине (х, у, z).

Повторяя те же рассуждения с каждой парой граней, мы получаем

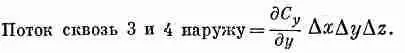
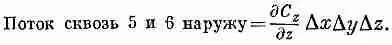
а

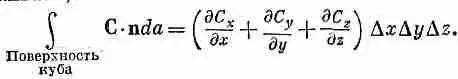
А общий поток через все грани равен сумме этих членов. Мы обнаруживаем, что

Сумма производных в скобках как раз есть С·С, a DxDyDz=DV (объем куба). Таким образом, мы можем утверждать, что для бесконечно малого куба