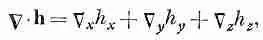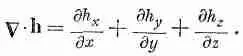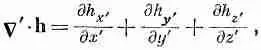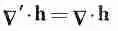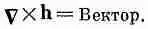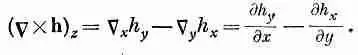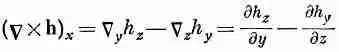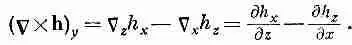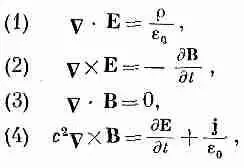Feynmann - Feynmann 5

§ 5. Операции с С

Можно ли с векторным оператором С производить другие алгебраические действия? Попробуем скомбинировать его с век­тором. Из двух векторов можно составить скалярное произве­дение, причем двоякого рода:

(Вектор)·С или С· (Вектор).

Первое выражение пока что ничего не означает — это все еще оператор. Окончательный смысл его зависит от того, на что он Судет действовать. А второе произведение — это некое скаляр­ное поле (потому что А·В — всегда скаляр).

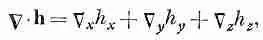
Попробуем составить скалярное произведение С на извест­ное поле, скажем на h. Распишем покомпонентно

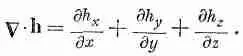
(2.32)

(2.33)

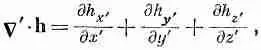
Эта сумма инвариантна относительно преобразования координат. Если выбрать другую систему (отмеченную штрихами), то получилось бы

(2.34)

а это — то же самое число, которое получилось бы и из (2.33), хотя с виду оно выглядит иначе, т. е.

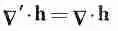
(2.35)

в любой точке пространства. Итак, С·h — это скалярное поле, и оно должно представить собой некоторую физическую вели­чину. Вы должны понимать, что комбинация производных в С·h имеет довольно специальный вид. Могут быть и другие комбинации всяческого вида, скажем dh y / dx , которые не яв­ляются ни скалярами, ни компонентами векторов.

Скалярная величина С· (Вектор) очень широко применяется в физике. Ей присвоили имя «дивергенция», или «расходимость». Например,

С·h = div h = «Дивергенция h». (2.36)

Можно было бы, как и для СT, описать физический смысл С·h. Но мы отложим это до лучших времен.

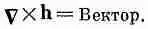
Посмотрим сначала, что еще можно испечь из векторного оператора С. Как насчет векторного произведения? Можно на­деяться, что

(2.37)

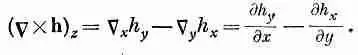
Компоненты этого вектора можно написать, пользуясь обыч­ным правилом для векторного произведения [см. (2.2)]:

(2.38)

Подобно этому,

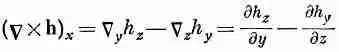
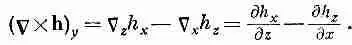
(2.39)

(2.40)

Комбинацию СXh называют «ротор» (пишут rot h), или (редко) «вихрь h» (пишут curl h ).Происхождение этого назва­ния и физический смысл комбинации мы обсудим позже.

В итоге мы получили три сорта комбинаций, куда входит С:

С Т = grad T = Вектор,

С·h=divh = Скаляр,

СXh = roth = Вектор.

Используя эти комбинации, можно пространственные вариации полей записывать в удобном виде, т. е. в виде, не зависящем от той или иной совокупности осей координат.

В качестве примера применения нашего векторного диф­ференциального оператора С выпишем совокупность вектор­ных уравнений, в которой содержатся те самые законы электро­магнетизма, которые мы словесно высказали в гл. 1. Их назы­вают уравнениями Максвелла.

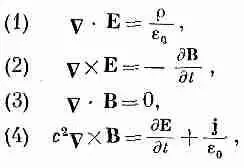
Уравнения Максвелла

(2.41)

где r (ро) — «плотность электрического заряда» (количество заряда в единице объема), a j — «плотность электрического тока» (скорость протекания заряда сквозь единицу площади). Эти четыре уравнения содержат в себе законченную классиче­скую теорию электромагнитного поля. Видите, какой элегант­ной и простой записи мы добились с помощью наших новых обозначений!

§ 6. Дифференциальное уравнение потока тепла

Приведем другой пример векторной записи физического закона. Этот закон не из точных, но во многих металлах и других материалах, проводящих тепло, он проявляется со­вершенно четко. Известно, что если взять плиту из какого-то материала и нагреть одну ее сторону до температуры Т 2 , а дру­гую охладить до Т 1 , то тепло потечет от T 2 к Т 1 (фиг. 2.7, а). Поток тепла пропорционален площади торцов А и разнице температур. Кроме того, он обратно пропорционален расстоя­нию между торцами. (Для заданной разницы температур чем тоньше плита, тем мощнее поток тепла.).