Feynmann - Feynmann 4a

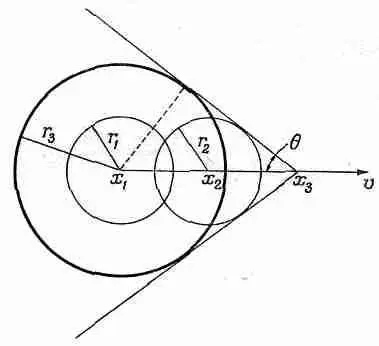
Фиг. 51.1. Фронт ударной волны, образующий конус с вершиной в источнике и углом полураствора q =arcsin ( c w / v ).

Когда источ­ник переместится еще дальше, в точку х 3 , и отсюда тоже пойдет волна, то волна из точки х 2 распространится в радиусе r 2 , а волна из точ­ки х 1 — в радиусе r 3 . Конечно, все это происхо­дит непрерывно, а не какими-то этапами, и по­этому получается целый ряд таких волновых колец с общей касательной линией, проходя­щей через центр источника. Мы видим, что источник, вместо того чтобы порождать сфери­ческие волны, как это произошло бы, будь он неподвижен, порождает фронт, образующий в трехмерном про­странстве конус или в двухмерном пару пересекающихся пря­мых линий. Из рисунка нетрудно найти угол между этими дву­мя линиями. За данный отрезок времени источник проходит расстояние, пропорциональное его скорости v , скажем х 3-х 1 . Тем временем фронт волны распространится на расстояние r 3, пропорциональное c w — скорости волны. Ясно поэтому, что си­нус угла полураствора равен отношению скорости волны к ско­рости источника, а это может быть только тогда, когда c w мень­ше v , или скорость объекта больше скорости волны:

sinq=c w/v. (51.1)

Интересно, что движущийся предмет вовсе не обязан быть источником звука, оказывается, что когда предмет движется быстрее скорости звука, то он сам производит звук. Ему для этого вовсе не обязательно вибрировать. Любой предмет, дви­жущийся через среду быстрее, чем эта среда переносит волны, будет автоматически порождать волны просто благодаря свое­му движению. Это проще понять для случая звука, но тоже самое происходит и со светом. Сначала может показаться, что ничто не может двигаться быстрее скорости света. Однако фа­зовая скорость света в стекле, например, меньше, чем в пустоте, а через кусок стекла можно пропустить такую частицу, ско­рость которой будет очень близка к скорости света в пустоте, тогда как фазовая скорость света в стекле может быть равна только 2/ 3этой скорости. Частица, летящая быстрее света в среде, порождает коническую световую волну с вершиной в источнике, подобно волнам, вызванным лодкой (эти волны одной и той же природы). Измеряя угол при вершине конуса, мы можем определить скорость частицы. В физике это исполь­зуется для измерения скорости частиц как один из методов оп­ределения их энергии при высокоэнергетических исследованиях. Единственное, что приходится измерять,— это направление излучения света.

Такое излучение называют излучением Черенкова, который первый наблюдал его. Тамм и Франк теоретически выяснили, насколько оно должно быть интенсивным. За эту работу этим ученым в 1958 г. совместно была присуждена Нобелевская премия.

Подобное же явление для случая звука показано здесь на фиг. 51.2; это фотография объекта, движущегося через газ со ско­ростью, превышающей скорость звука.

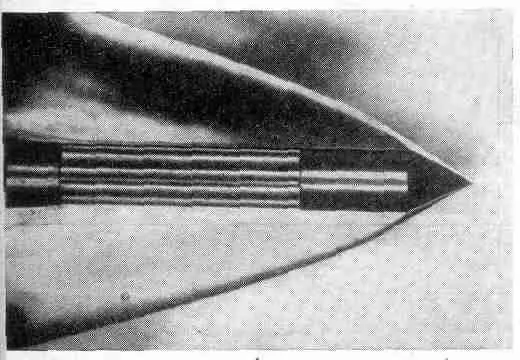
Фиг. 51.2. Ударная волна в газе, вызванная сна­рядом, движущимся бы­стрее звука.

Изменение в давлении приводит к изменению показателя преломления, поэтому гра­ницу волн с помощью специальной оптической системы можно сделать видимой. Итак, предмет, движущийся быстрее скорости звука, действительно дает коническую волну. Однако при бо­лее внимательном рассмотрении оказывается, что граница на самом деле искривлена. В асимптотике это действительно пря­мая линия, но вблизи вершины она искривлена, и сейчас мы обсудим, отчего так может получаться. Это непосредственно приводит нас ко второй теме данной главы.

§ 2. Ударные волны

Зачастую скорость волны зависит от ее амплитуды, и в слу­чае звука эта зависимость возникает следующим образом. Движущийся в воздухе предмет должен сдвигать его со своего пути, вызывая при этом возмущение в виде какой-то ступенча­той функции давления, причем давление за волновым фронтом оказывается выше, чем в невозмущенной области, т. е. в обла­сти, куда волна (которая распространяется с нормальной ско­ростью) еще не добралась. Воздух за волновым фронтом оказы­вается адиабатически сжатым, поэтому температура его будет выше, чем перед фронтом. Но скорость звука с температурой увеличивается, поэтому в области позади скачка она оказы­вается больше скорости звука впереди него.