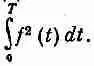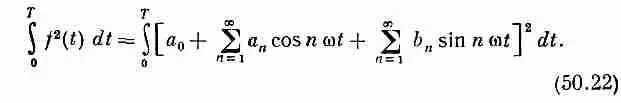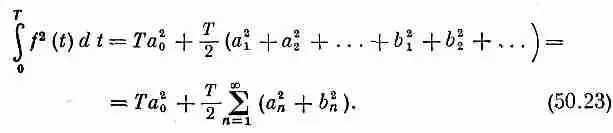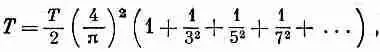Feynmann - Feynmann 4a

Сумма этого ряда равна p/4, а, стало быть, f ( T )=1 .

§ 5 . Теорема об энергии

Энергия волны пропорциональна квадрату ее амплитуды.

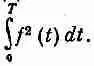
Для сложной волны энергия за один период пропорциональна m

Эту энергию можно связать с коэффициентами Фурье.

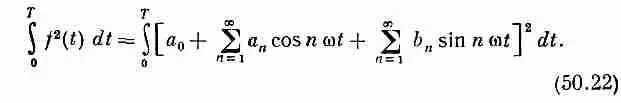
Напишем

После раскрытия квадрата в правой части мы получим сумму всевозможных перекрестных членов типа a 5cos5wtb 7cos7wt. Однако выше мы уже показали [уравнения (50.11) и (50.12)], что интегралы от всех таких членов по одному периоду равны нулю, так что останутся только квадратные члены, подобные a 2 5 cos 2 5 w t . Интеграл от любого квадрата косинуса или синуса по одному периоду равен Т/2, так что получаем

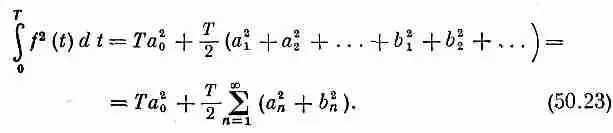
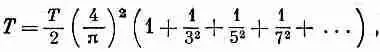
Это уравнение называют «теоремой об энергии», которая гово­рит, что полная энергия волны равна просто сумме энергий всех ее фурье-компонент. Применяя, например, эту теорему к ряду (50.19), мы получаем

поскольку [ f ( t ) ] 2 = 1 . Таким образом мы узнали, что сумма квад­ратов обратных нечетных чисел равна p 2 /8. Точно так же, выпи­сав сначала ряд Фурье для функции и используя затем теорему об энергии, можно доказать результат, понадобившийся нам в гл. 45, т. е. что 1+ 1/2 4+ 1/3 4+... равно p 4/90.

§ 6. Нелинейная реакция

Наконец, в теории гармоник есть одно очень важное явление, которое необходимо отметить, учитывая его практическую важ­ность, но это уже относится к области нелинейных эффектов. Во всех рассмотренных нами до сих пор системах все предпола­галось линейным; реакция на действие силы, например пере­мещение или ускорение, всегда была пропорциональна силам. Токи в электрической цепи были тоже пропорциональны на­пряжениям и т. д. Теперь мы хотим рассмотреть случаи, когда строгая пропорциональность отсутствует. Представим на ми­нуту устройство, реакция которого x выход=x выхв момент t опре­деляется внешним воздействием x вход= x вхв тот же момент t .

Например, x вхможет быть силой, а х вых— перемещением, или х вх — ток, а x вых— напряжение. Если бы устройство было ли­нейное, то мы бы получили

x вых ( t )= Kx вх ( t ), (50.24)

где К — постоянная, не зависящая ни от t , ни от х ек . Предполо­жим, однако, что устройство только приблизительно линейное, т. е. на самом деле нужно писать

x вых(t)=K[x вх(t)+ex 2 вх(t)]. (50.25)

где e мало по сравнению с единицей. Такие линейная и нелиней­ная реакции показаны на фиг. 50.4.

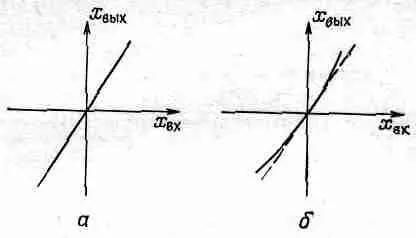
Фиг. 50.4. Реакции, а — линейная,

x вых = kx вх ; б—нелинейная, x вых = k ( х вх + e x 2 вх ).

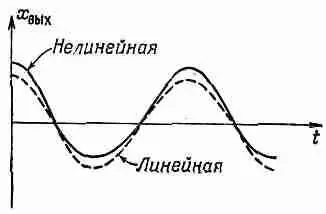
Нелинейная реакция приводит к нескольким важным прак­тическим следствиям. Некоторые из них мы сейчас обсудим. Посмотрим сначала, что получается, если пропустить через по­добное устройство «чистый» тон. Пусть x вх = cos w t . Если мы по­строим график зависимости x выхот времени, то получим сплош­ную кривую, показанную на фиг. 50.5.

Фиг. 50.5. Реакция нелинейного устройства на входящий сигнал cosw t .

Для сравнения показана линейная реак­ция.

Для сравнения там же проведена пунктирная кривая, представляющая реакцию ли­нейной системы. Мы видим, что на выходе получается уже не косинусообразная функция. Она более острая в вершине и более плоская в основании. Поэтому мы говорим, что выходной сигнал искажен. Однако, как известно, такая волна не будет уже чистым тоном, а приобретает какие-то высшие гармоники Можно найти эти гармоники. Подставляя x вх=coswt в уравнение (50.25), получаем

х вых =К ( cos w t + e cos 2 w t ). (50.26) Используя равенство cos 2q = 1/ 2(l-cos2q), находим